 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Squash



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
In the game of squash, the player who serves is the only player who can win the next point. If the server loses the rally, no points are scored and the other player serves next. Note that if in two consecutive rallies both servers lose the rally, then the situation is exactly the same as it was before the two serves. This is not taken into account below where the tree diagram and solution from Allan Ling apply to the simpler problem where the player who wins a rally wins the point whether serving or receiving. Can you see how to re-draw the tree diagram to give the solution for the game of squash?
If I call '9', then I win with probability p.
If I call '10', then there are 6 possible outcomes, shown by the tree diagram. 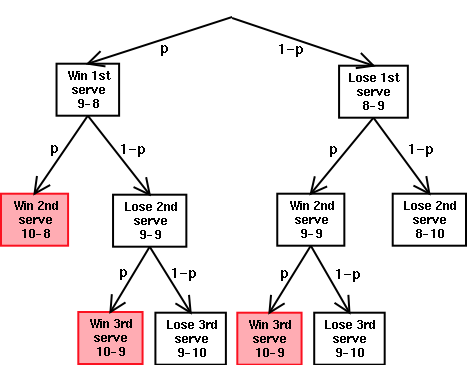
The winning outcomes are shown in red. Calculating the probabilities of these three outcomes, we find that the total is p 2 + p(1-p)p + (1-p)p 2 = 3p 2 - 2p 3 .
Now we compare this to p to see which is larger.
When p< 0.5, then p> 3p 2 -2p 3 .
When p=0.5, then p=3p 2 -2p 3 .
When p> 0.5, then p< 3p 2 -2p 3 .
Therefore, in this simplified situation, if p is smaller than 0.5, I should call '9', and if p is greater than 0.5, I should call '10'. If p=0.5, I have an equal chance of winning on both choices.
Now what happens playing according to the rules of squash?