Four Points on a Cube

Congratulations to Ang Zhi Ping from River Valley High School, Singapore for this solution.

Take the vertex of the cube at the origin $(0,0,0)$ as shown in the diagram. The tetrahedron has vertices $O,X,Y,Z$, where the three centres $X$, $Y$ and $Z$ are as follows: $$ X=\left(1,\frac{1}{2},\frac{1}{2}\right), Y=\left(\frac{1}{2},1,\frac{1}{2}\right), Z=\left(\frac{1}{2},\frac{1}{2},1\right). $$

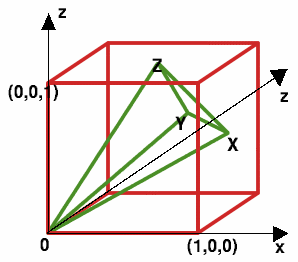
The area required is the sum of the areas of the triangles $XYZ$ (which is equilateral), and $OXY$, $OYZ$, $OZX$ (which are congruent to each other and isosceles).

Now $XY= 1/\sqrt{2}$ so that $$ area(XYZ) = \frac{1}{2} \left(\frac{1}{\sqrt{2}}\right)^2 \sin 60^\circ = \frac{\sqrt{3}}{8} $$ Next, $$ OX = OY = OZ = \sqrt{\frac{3}{2}}. $$ Thus $$ OX = OY = \sqrt{\frac{3}{2}}, XY = \frac{1}{\sqrt{2}}. $$ This gives the area of $OXY$ as $\sqrt{11}/8$. Thus the surface area of the tetrahedron is $$ \frac{\sqrt{3}}{8} + \frac{3\sqrt{11}}{8}. $$