There were a few complete solutions sent in and many who showed us what the final result at the tables would be, i.e. $5$ at the $1$ table, $10$ at the $2$ table and $15$ at the $3$ table.

The full solution showing fractions at each stage were received from Adriel, Emily and Aswaath from the Garden International School in Maylasia. Also Daniel at Staplehurst School and Megan at Twyford School. Here is Emily's contribution.

So after child $9$ has sat down, there are now:
$2$ people at table $1$
$3$ people at table $2$
$4$ people at table $3$
This is a list of which table child $10-30$ would go to:
The reason I listed down which table they would go to is to see whether there was a pattern
Child $10$ would go to table $3$ and receive $ ¾$ of the chocolate
Child $11$ would go to table $3$ and receive $ ½$ of the chocolate
Child $12$ would go to table $2$ and receive $ ½$ of the chocolate
Child $13$ would go to table $3$ and receive $3/7$ of the chocolate
Child $14$ would go to table $2$ and receive $2/5$ of the chocolate
Child $15$ would go to table $3$ and receive $3/8$ of the chocolate
Child $16$ would go to table $1$ and receive $1/3$ of the chocolate
Child $17$ would go to table $3$ and receive $1/3$ of the chocolate
Child $18$ would go to table $2$ and receive $1/3$ of the chocolate
Child $19$ would go to table $3$ and receive $3/10$ of the chocolate
Child $20$ would go to table $2$ and receive $2/7$ of the chocolate
Child $21$ would go to table $3$ and receive $3/11$ of the chocolate
Child $22$ would go to table $1$ and receive $ ¼$ of the chocolate
Child $23$ would go to table $2$ and receive $ ¼$ of the chocolate
Child $24$ would go to table $3$ and receive $ ¼$ of the chocolate
Child $25$ would go to table $3$ and receive $3/13$ of the chocolate
Child $26$ would go to table $2$ and receive $2/9$ of the chocolate
Child $27$ would go to table $3$ and receive $3/14$ of the chocolate
Child $28$ would go to table $1$ and receive $1/5$ of the chocolate
Child $29$ would go to table $2$ and receive $1/5$ of the chocolate
Child $30$ would go to table $3$ and receive $1/5$ of the chocolate
So now there are:
$5$ people in table $1$
$10$ people in table $2$
$15$ people in table $3$
I found out a pattern from child 10 to child $30$. When it was child $16$'s turn to decide which was the best place to sit, child $16$ could just choose to randomly sit on any table because he'll still get $1/3$ of the chocolate in any of the tables. Same with child $22$ and $28$. Child $22$ would either ways get $ ¼$ and child $28 1/5$. The numbers also increase by $6. 16, 22, 28$.
I noticed that sometimes there were tables that shares the same amount of chocolate so you could choose randomly between $2$ or all of the tables which was what I did when I tried finding out how many chocolates each child receives as they go to find the best table for them
For example: Child $16$ gets to choose between any of the $3$ tables because he'll still get $1/3$ of the chocolate in any of the tables.

Martino, Guglielmo, Lorenzo and Virginia at the International School of Turin in Italy sent us a picture of their final solution for 30 children:


 

Yinyi who goes to the Chinese International School, sent us this picture of the table he made to work on the solution:

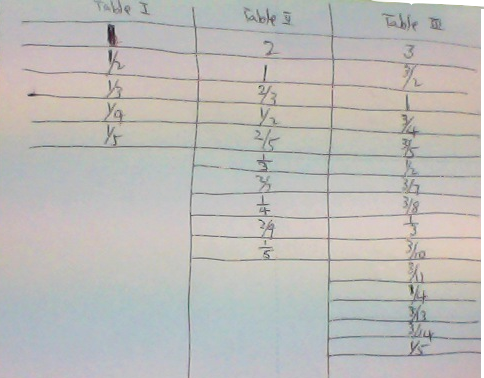
We were sent in several solutions from the children at Clearwater Bay School in Hong Kong - thank you all for sharing your ideas with us. Charlotte and Jasper sent in this table showing their solution:

Well done for working this out! I wonder if anybody can spot the pattern in this solution?

Finally, thank you to Sam and Jack from Orchard Junior School who sent in a table of their solution for a class of 24 children.  Sam and Jack chose to represent the fractions of chocolate as decimal numbers but unfortunately, I think you made a little slip-up for the last four pupils in the class.

Well done all of you for your work on quite a difficult challenge.