 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
On the Road



- Problem
- Student Solutions
- Teachers' Resources
This solution was sent in by Ben at Madras College in St Andrews. Another good solution was sent in by Nicola at Madras College.
The car overtakes the scooter at 12.00. This point can be taken as the origin of a graph of distance against time.
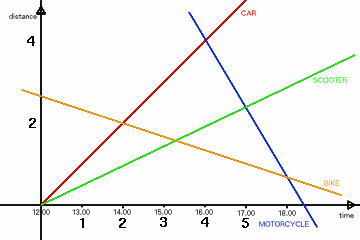
Assuming that the car travels at 1 unit per hour, the car therefore has equation y=x.
Now assume that the scooter travels at $a$ times the speed of the car, where $0 < a < 1$. So, it has equation $y=ax$.
Now for the motorcycle, whose line goes through $(4,4)$ and $(5,5a)$.
Gradient $= (5a-4)/(5-4) = 5a-4$
Substituting in the point $(5,5a)$,
$$ \begin{eqnarray} y - b &=& m(x-a) \\ y - 5a &=& (5a-4)(x-5) \\ y &=& 5ax - 4x - 20a + 20 \end{eqnarray} $$
To find the intersection of the motorcycle and bike, we know that $x=6$.
Therefore $y-5a = (5a-4) \times 1$, and so $y = 10a-4$.
For the bike,
$$ gradient = \frac{10a-4-2}{6-2} = \frac{10a-6}{4} $$
$$ \begin{eqnarray} y -b &=& m(x-a) \\ y - (10a-4)& =& \frac{10a-6}{4}(x-6) \\ 4y - 40a + 16 &=& 10ax - 6x - 60a + 36 \\ 4y &=& 10ax - 6x - 20a + 20 \\ \end{eqnarray} $$
When the bike meets the scooter, $y=ax$, so $4y=4ax$.
Therefore
$$ \begin{eqnarray} 10ax - 6x - 20a + 20 &=& 4ax \\ 6ax - 6x &=& 20a - 20 \\ 3ax - 3x &=& 10a - 10 \\ 3x(a-1) &=& 10(a-1) \\ 3x &=& 10 \\ x &=& 3\frac{1}{3} \end{eqnarray} $$