You may also like

problem icon

Telescoping Series

Find $S_r = 1^r + 2^r + 3^r + ... + n^r$ where r is any fixed positive integer in terms of $S_1, S_2, ... S_{r-1}$.

problem icon

Growing

Which is larger: (a) 1.000001^{1000000} or 2? (b) 100^{300} or 300! (i.e.factorial 300)

problem icon

Climbing Powers

$2\wedge 3\wedge 4$ could be $(2^3)^4$ or $2^{(3^4)}$. Does it make any difference? For both definitions, which is bigger: $r\wedge r\wedge r\wedge r\dots$ where the powers of $r$ go on for ever, or $(r^r)^r$, where $r$ is $\sqrt{2}$?

How Many Solutions?

Stage: 5 Challenge Level: Challenge Level:1

This is a 'quickie'.

Ling Xiang Ning of Raffles Institution in Singapore, found two solutions, and after trying some more values of x, decided that there would be no more because:
"The graphs of $y = x$ and $y = (\sqrt {2})^x$ cut at exactly two points $(2, 2)$ and $(4, 4)$ so there are exactly two solutions."

Vassil from Lawnswood High School in Leeds, used a different graph to convince himself that there were no more solutions.
First of all, he rearranged the equation:


$$ \eqalign { x &=& (\sqrt{2})^x \\ \sqrt[x]{x} &=& \sqrt{2} }$$ (taking the $x^{th}$ root)

$$ \eqalign { (\sqrt[x]{x})^2 &=& 2 \\ x^{\frac{2}{x}} &=& 2 } $$ (squaring).


Next he calculated values of $x^{\frac{2}{x}}$ from $1$ to $8$, and plotted this graph:


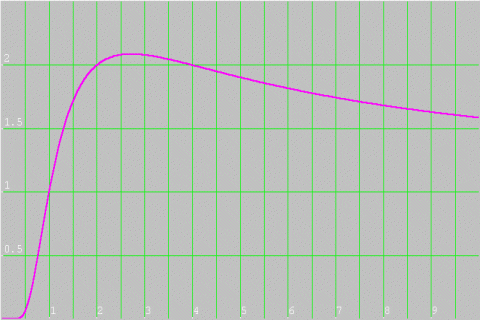
Vassil commented that by looking at the original equation we could rule out negative values of $x$, and that the values in the graph decline after $x=4$. The justification for the decline is that we are calculating smaller and smaller powers. However, you may not be convinced, as the number we are finding powers of is getting bigger. Are you sure that curve isn't going to go up again further along?

The use of a graph to justify there being only 2 solutions was a good idea.

Clearly $x=0$ is not a solution and there are no negative solutions because the right hand side is positive. We have found 2 solutions $x=2$ and $x=4$ and we have to show that there are no other solutions.

Consider the function $f(x) = (\sqrt 2)^x = exp(x\ln \sqrt 2)$. Differentiating the function gives: $$\frac{df}{dx} = (ln \sqrt 2)\times exp(x\ln \sqrt 2)$$ and $$\frac{d^2f}{dx^2} = (ln \sqrt 2)^2\times exp(x\ln \sqrt 2)> 0.$$ So the graph of f is convex (the first derivative, or gradient, is always increasing) so the graph of $y=f(x)$ meets $y=x$ in at most 2 points. So $2$ and $4$ are the only solutions.

The NRICH Project aims to enrich the mathematical experiences of all learners. To support this aim, members of the NRICH team work in a wide range of capacities, including providing professional development for teachers wishing to embed rich mathematical tasks into everyday classroom practice. More information on many of our other activities can be found here.
Copyright © 1997 - 2012. University of Cambridge. All rights reserved.
NRICH is part of the family of activities in the Millennium Mathematics Project.