Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Stonehenge
Age 16 to 18
Challenge Level 





- Problem
- Getting Started
- Student Solutions
Here's a good clear explanation from Jack of Madras College.
Consider the movement of the block relative to the logs:
When the log makes one revolution it travels ${\pi}d$ metres. As the block is in contact with the logs, it moves ${\pi}d$ metres along the horizontal plane.
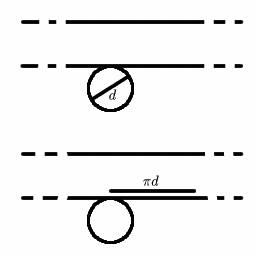
Therefore, the block moves ${\pi}d$ metres relative to the logs.
Now consider the movement of the logs relative to the ground:
When the log makes one revolution it rotates ${\pi}d$ metres. As it is in contact with the ground it moves ${\pi}d$ metres along the horizontal plane.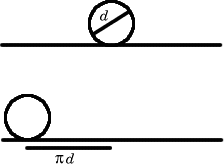
Therefore, the log moves ${\pi}d$ metres relative to the ground.
This means the log moves ${\pi}d$ metres relative to the
ground but the block moves ${\pi}d$ metres relative to the
logs.
Therefore, the block moves $2{\pi}d$ metres relative to the
ground, which is twice as much as the logs.
Thus:- the block
moves twice as fast as the logs .