Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Plane to See
Age 16 to 18
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
The problem can be solved, without using 3D coordinates, by essentially the same argument as the one used in the solution below. You have to locate the same points, and use similar triangles and the volumes of similar tetrahedra.
This solution came from Brad of Kokomo School, India and a very similar solution fromSue Liu of Madras College, St Andrews.
Using 3D coordinates with point $A$ at the origin, $B$ being the point $(4, 0, 0)$, $C$ the point $(4, 4, 0)$, $D$ the point $(0, 4, 0)$, $E$ the point $(0, 0, 4)$ etc as shown in the diagram. The point $P$ which is the midpoint of $AB$ has coordinates $(2, 0, 0)$ and $Q$, which is a quarter of the way along $EF$ has coordinates $(1, 0, 4)$.
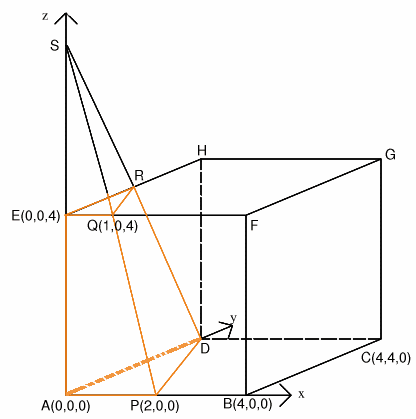
The general equation of a plane is $ax + by + cz = 1$ and to find $a$, $b$ and $c$ we only need to know three points in the plane. Hence it is easy to find the equation of the plane through $D$, $P$ and $Q$. Substituting the coordinates of the points into the equation of the plane we get:
$ 4b = 1 $
$ 2a = 1 $
$ a + 4c = 1 $
This gives $a = 1/2$, $b = 1/4$ and $c = 1/8$. Writing the equation of the plane without fractions we get $$4x + 2y + z = 8.$$ The point $R$ where the plane cuts the line $EH$ has coordinates $(0, y, 4)$ where $0 + 2y + 4 = 8$ so $R$ is the point $(0, 2, 4)$.
Now $RE = 2$, $EQ = 1$, $\angle \rm{ REQ} = 90^\circ$, and DA = 4, AP = 2, $\angle \rm{ DAP} = 90^\circ$ so it follows that the triangles $REQ$ and $DAP$, which lie in parallel planes, are similar. Also, if we extend the lines $AE$, $PQ$ and $DR$ they will meet at one point $S$ where $SE = 4$ and $SA = 8$.
The points $S$, $A$, $P$ and $D$ are the vertices of a tetrahedron which is sliced into two parts by the plane through $R$, $E$ and $Q$. The required volume of the section of the cube is given by subtracting the volume of the tetrahedron $SEQR$ from the volume of the tetrahedron $SAPD$.
Volume of smaller section of cube
$ = {1\over 3}(32 - 4) = {28\over 3}. $
The volume of the whole cube is $64$ cubic units so the ratio of the volume of the smaller piece to the volume of the cube is $7$ to $48$. The ratio of the volumes of the two pieces of the cube is $7$ to $41$.