Mean Geometrically

A and B are two points on a circle centre O. Tangents at A and B cut at C. CO cuts the circle at D. What is the relationship between areas of ADBO, ABO and ACBO?

Golden Triangle

Three triangles ABC, CBD and ABD (where D is a point on AC) are all isosceles. Find all the angles. Prove that the ratio of AB to BC is equal to the golden ratio.

Sangaku

The square ABCD is split into three triangles by the lines BP and CP. Find the radii of the three inscribed circles to these triangles as P moves on AD.

So Big

Stage: 5 Challenge Level:

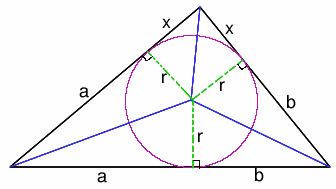
Eduardo from the British School, Manila, Tomas from Malmesbury School and Philip used the tangent formula and Alex and also Sue Liu of Madras College, St Andrew's sent a solution to this problem which depends on the use of Heron's Formula for the area of a triangle. Well done all of you.

FIRST METHOD

Using the tangents of the angles at the centre of the circle and the formula

$\tan X= -\tan(A + B) =\frac{\tan A + \tan B} {\tan A \tan B - 1} $ where $A + B + X = 180^o$,

$\frac{x}{r}= \frac{\frac{a}{r} + \frac{b}{r}}{\frac{ab}{r^2}-1} = \frac{r(a + b)}{ab - r^2}.$

The area of the triangle is

$(a + b + x)r = (a + b)r + \frac{r^3(a + b)}{ab - r^2}= \frac{(a + b)abr}{ab - r^2}$ as required.

SECOND METHOD
This method uses Heron's formula. The lines from the centre of the circle to the edges each meet the tangents to the circle forming right angles as shown. The triangle has been rotated/reflected so that the side with length (a+b) is the base. (However it is rotated it is the same shape of unknown angles and lengths). As the tangents to a circle from an external point are equal in length (easily proved using congruent triangles) the other lengths of the sides of the triangle can be found. The incircle divides the sides of the triangle into lengths $c' = a + b$, $b' = b + x$ and $a' = x + a$ as shown in the diagram.

The semi-perimeter of the triangle is given by $s = x + a + b$ and from Heron's formula the area of the triangle is

$A = \sqrt{(s(s - a')(s - b')(s - c'))}$

$= \sqrt{((a + b + x)abx)} $

Also, the triangle is divided into three smaller triangles and the total area is given by

$ A = \frac{1}{2}(a + b)r + \frac{1}{2}(b + x)r + \frac{1}{2}(x + a)r $

$=(a + b + x)r $.

Equating the two answers

$ \sqrt{abx(a + b + x)} = (a + b + x)r $

$ abx(a + b + x) = (a + b + x)^2 r^2 $

$ abx = (a + b + x)r^2 $

$x = \frac{(a + b)r^2}{ (ab - r^2).} $

Hence

$ A = (a + b + x)r$

$ = \frac{r((a + b)(ab - r^2) + (a + b)r^2)}{ ab - r^2}$

$ = \frac{abr(a + b)}{ab - r^2.} $

An alternative method, not using Heron's formula, is based on finding $x$ in terms of $a$ and $b$ using the tangents of the angles at the centre of the circle.