Tea Cups

'Tea Cups' printed from https://nrich.maths.org/

Show menu

We had a few good solutions to this challenge. Firstly from The Blue Coat Primary School in Wotton-Under-Edge

First I would put all the combinations together, then I'd line up all the double colour combinations together (red, red, white, white, green, green, blue, blue). After that I put all of the red tops diagonally and the blue tops. I found it easier by spacing my cubes out, in my diagonal rows the saucer couldn't be the same as my double saucer, so I had to look really carefully according to the rules. Finally I filled the rest in by always having only one of every colour in each row and column.
My tip is to look at the problem in a different way :).

Next, from Eliza at St. Joseph's School in Australia

To start with I drew a 4 x 4 grid. In the grid I placed 4 saucers of each colour so that It matched the criteria. When they were done I placed the tea cups on top so that there was only one green on red and only one red on green and so on. Then I had four tea cups left and I places them on their own colour. Once I had placed the cups on their correct saucers I went through and check and double checked. This is how I did tea cups.

ï¿¼

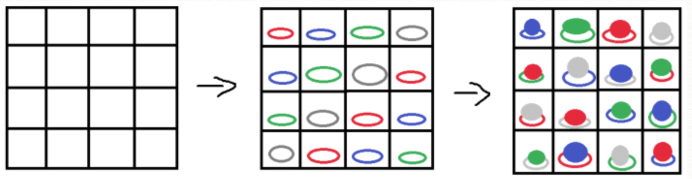
Then, from Grace from Birdwood Primary in Australia

I used some counters and a grid that was four squares long and four squares wide. I placed counters for the saucers first and realised that I couldn't have the same colour counter on the diagonal. So I placed different colour counters on the diagonals. Then I worked out where the remaining counters had to go. All of the counters for the saucers were placed and checked to see that there were no counters the same colour in each row and column. I then placed the red cups on one diagonal and the white cups on the other diagonal. I then placed the blue and green cups. I then checked my work.
The picture seems to indicate that the coloured counters were replaced to give an interesting picture!

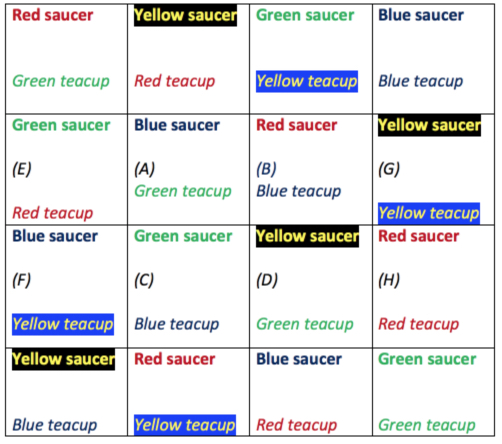
Next from Andrew from Dulwich College in Singapore

Explanation:
You would want to create the 2 main diagonals (the 4 square ones)matched up with the same teacup or saucer. Then once that's done, find the lower diagonal square of Position A (which is the upper diagonal square is position F) and put in the same saucer in F as you did in A. Do the same thing for Position B and H. They can be random teacups for those 4 positions, but not for C,E,D and G. Match the same saucer for the upper diagonal square for Position C (which the upper diagonal square is position E), but MAKE SURE THAT THE TEACUPS MATCH. Do exactly the same for positions D and G. Then, do the remaining squares on the outside matching the saucers but at the same time making sure that the teacups match, as this is crucial. Once you have done the outside, this should be done and if they are still mistakes, take out all the mistaken squares out and re-arrange them with diagonals so they match, although if you did everything carefully and accurately, there should be no need for this bonus step. By the time you do all of this, you should have a beautiful, satisfying square of 16 saucers and teacups. Lovely, isn't it?

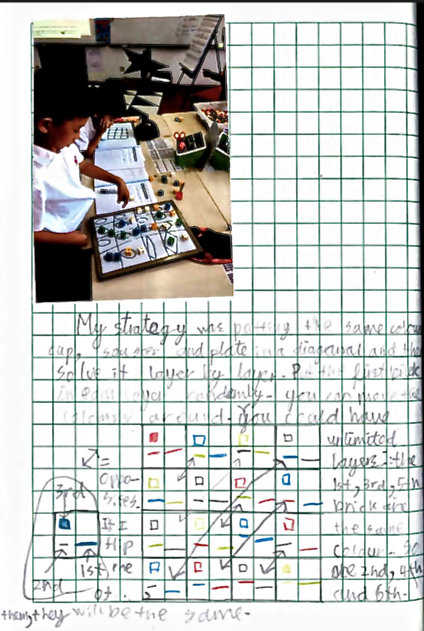
Next, here's Dylan's work sent in by the teacher from Dulwich College in Beijing China

Here is a solution from Dylan at an international school in Beijing. We spent two lessons exploring patterns and moved onto looking at 3 layers (including a plate). Dylan managed to discover the patterns with rotating opposite cups and saucers to reach the combinations. He also ensured that the diagonal line had the same coloured cup and saucer as this was his
first strategy to solving the problem.

Finally Sam from Raymond Park Middle School in the USA

Well done all of you these are wonderful solutions.