Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Bendy Quad
Age 14 to 16
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
The first thing some solvers did was to play with the interactivity to see what things they could change and what they couldn't.
Playing with the interactivity told us that if we change one thing, we can't change anything else without affecting the thing we changed first. For example, we moved point B to change the angle at A, and this then fixed the rest of the shape (when we tried to move C, the angle at A changed). We checked why this was the case by constructing the shape with ruler and compasses. If we picked a particular angle at A, there was only one possible quadrilateral with the correct lengths. We thought about this in terms of the two triangles ABD and BCD. This links to our work on congruent triangles.
We then started to investigate the shapes we could make.
The smallest that angle A can be is just above $0^{\circ}$ giving a long thin quadrilateral:
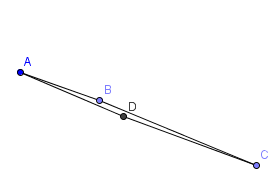
Angle C is also very close to $0^{\circ}$, and angles B and D are both very close to $180^{\circ}$.
Then we made angle A as big as we could. If it went over $180^{\circ}$ the quadrilateral would no longer be convex and if it was equal to $180^{\circ}$ we would have a triangle. This picture shows what the shape looks like when angle A is close to $180^{\circ}$
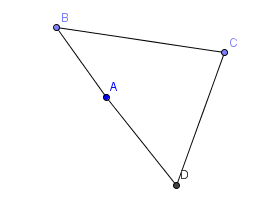
When angle A is $180^{\circ}$, angles B and D are as small as they can possibly be, and angle C is as large as it can possibly be. If we tried to make B and D smaller or make C bigger, A got bigger too.
We drew the shape as a triangle to help us to work out the minimum values of B and D, and the maximum value of C.
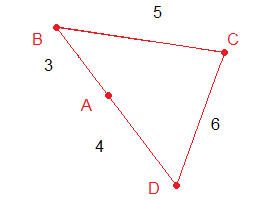
BCD is a triangle with sides $7$, $6$ and $5$ units.We used the Cosine Rule to work out angle B.
${CD}^2 = {BC}^2 +{BD}^2-2(BD)(CD)cosB$
$6^2=5^2+7^2-2 \times 5 \times 7 \times cosB$
We rearranged this to get
$$ cos B = 0.543$$
which gave $$B = 57.1^{\circ}$$
Then we worked out angles C and D in the same way.
Angle C is $78.5^{\circ}$ and angle D is $44.4^{\circ}$ (all our numbers have been rounded to $3$ significant figures).
| This shows that all the quadrilaterals will have angle A between 0 and 180, B between 57.1 and 180, C between 0 and 78.5 and D between 44.4 and 180. Can you find any special quadrilaterals with angles in these ranges? Are there any with right angles in? Any cyclic quadrilaterals? We would love to hear about anything interesting you discover! |
|