Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Bendy Quad
Age 14 to 16
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
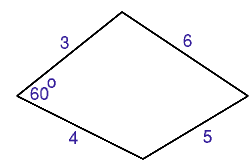
Suppose the angle $s$ is $60$ degrees, then it is easy to calculate the length of the diagonal and from that to calculatethe opposite angle in the diagram.
You might like to check your answer by drawing the quadrilateral accurately, using ruler and compasses only, and then measuring the angles.
Calculate the other angles of the quadrilateral.
Now calculate the angles of the cyclic quadrilateral formed by keeping the lengths of the sides the same and changing the angles so that opposite angles add up to 180 degrees. You might wish to use a spreadsheet.
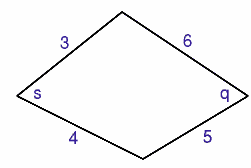 |
The question states that the quadrilateral is convex; this
means that the angles $s$ and $q$ are at most $180$ degrees.
Imagine moving the rods to make the angle $s$ as large or as
small as possible. Find the largest and smallest values of $s$ and
$q$.
|
To calculate the angles of the cyclic quadrilateral formed by
keeping the lengths of the sides the same and changing the angles
so that opposite angles add up to $180$ degrees you simply need to
use the fact that, in this case, $\cos s = - \cos q$.