You may also like

Cut Cube

Find the shape and symmetries of the two pieces of this cut cube.

Cushion Ball

The shortest path between any two points on a snooker table is the straight line between them but what if the ball must bounce off one wall, or 2 walls, or 3 walls?

Plane to See

P is the midpoint of an edge of a cube and Q divides another edge in the ratio 1 to 4. Find the ratio of the volumes of the two pieces of the cube cut by a plane through PQ and a vertex.

Napoleon's Hat

Age 16 to 18
Challenge Level

hat
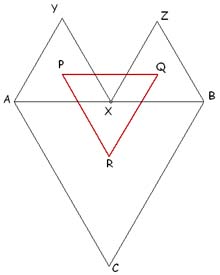The diagram shows three equilateral triangles $ABC, AYX$ and $XZB$. The point $X$ is a moveable point on $AB$. The points $P$, $Q$ and $R$ are the centres of the three triangles.

Experiment with the dynamic diagram.

What can you say about triangle $PQR$?

Can you prove your conjecture?

Created with GeoGebra

You can download your own free copy of Geogebra from the above link and draw your own dynamic diagrams.
The NRICH Project aims to enrich the mathematical experiences of all learners. To support this aim, members of the NRICH team work in a wide range of capacities, including providing professional development for teachers wishing to embed rich mathematical tasks into everyday classroom practice.
Copyright © 1997 - 2023. University of Cambridge. All rights reserved.
NRICH is part of the family of activities in the Millennium Mathematics Project.