Copyright © University of Cambridge. All rights reserved.
'Areas and Ratios' printed from https://nrich.maths.org/
Show menu
Areas and Ratios printable sheet - with clues
Areas and Ratios printable sheet - without clues
In the diagram below (which is not drawn to scale), the area of the three triangular regions is given.
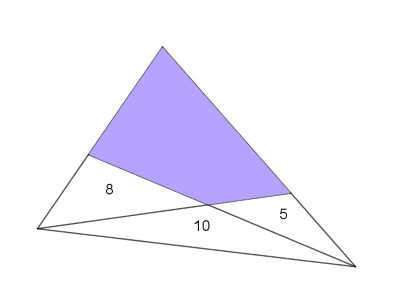
Can you work out the area of the shaded quadrilateral?
Perhaps it feels as though there isn't enough information to solve this problem!
If you are stuck, click below to reveal some suggestions that may help you.
First suggestion:
In the GeoGebra applet below, you can move the dots to create different triangles with bases which lie on the same straight line and with a shared apex.
What is the relationship between the ratio of the two areas and the ratio of the two lengths?
Can you explain why?
Can you apply this to the original problem?
Second suggestion:
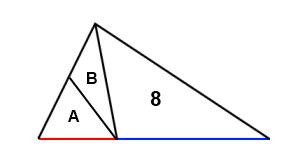
The red line is half the length of the blue line. Numbers and letters inside a triangle represent its area. What can you say about $A+B$?
Third suggestion:
It might be useful to label the points in the diagram. You could also split the quadrilateral into two triangles, and label them:
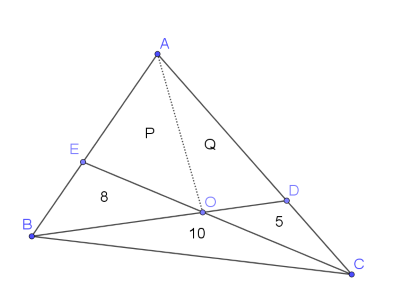
Can you use the ideas from the first two suggestions to write down some relationships in terms of P and Q?