Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Polycircles
Age 14 to 16
Challenge Level 





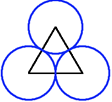
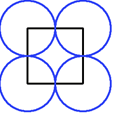
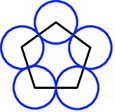
For any regular polygon it is always possible to draw circles with centres at the vertices of the polygon, and radii equal to half the length of the edges, to form a "polycircle" in which each circle just touches its neighbours.
Investigate and explain what happens in the case of non-regular polygons. Is it always possible to construct three circles with centres at the vertices of the triangle so that the circles just touch?
Try a numerical example, say the 3 points give a triangle of sides 12, 15 and 13. Find the radii of the circles.
Now use the same method when the sides of the triangle are $a$, $b$ and $c$.
Generalise still more! What about 4 circles around a quadrilateral? 5 circles around a pentagon? $n$ circles around an n-gon?
You may wish to use GeoGebra to explore.