Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Incircles
Age 16 to 18
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
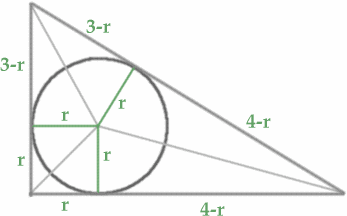
Ruoyi Sun, Sarah and Elizabeth from the North London Collegiate School Puzzle Club sent this neat solution.
"We found that by drawing the angle bisectors to find the centre of the incircle, and then drawing in 3 radii, we had created three pairs of congruent triangles. Therefore we found that part of the hypotenuse of the 3-4-5 triangle must have length $4-r$ and the other part $3-r$. We formed an equation $$3 - r + 4 -r = 5$$ hence $r = 1.$ For the 5-12-13 triangle the equivalent formula is $$5 - r + 12 - r = 13$$ and hence $r = 2.$"
Sue Liu of Madras College went further to find a formula for other Pythagorean triples for right angled triangles with incircles of radius $k$ for any integer $k$ and this is Sue's method.
"Clearly the largest circle that fits into a triangle is the incircle where the circle touches the three sides of the triangle. For a right angled triangle we can draw radii of length $r$ from the centre of the incircle perpendicular to each of the three sides $a$, $b$ and $c$. By equating areas we get $${1\over 2}ar +{1\over 2}br +{1\over 2}cr ={1\over 2}ab.$$ $$r = {ab\over a + b + c}.$$ For the 3-4-5 triangle $r = 12/(3 + 4 + 5) = 1$ so the incircle has radius 1. For the 5-12-13 triangle $r = 60/(5 + 12 + 13) = 2$ and the inradius is 2. The next part of the question asks us to find right angled triangles with incircle radius 3 and sides which are a primitive Pythagorean triples. Pythagorean triples ${a, b, c}$ are given parametrically by $$a = 2mn, \ b = m^2 - n^2, \ c = m^2 + n^2$$ where the integers $m$ and $n$ are coprime, one even and the other odd, and $m> n.$ We can consider a triangle with side lengths $2mn, \ m^2 - n^2, \ m^2 + n^2$ Again by equating areas as before, $${1\over 2} (2mnr + (m^2 - n^2)r + (m^2 + n^2)r) = {1\over 2}(m^2 - n^2)2mn$$ Hence $$r = {2mn(m^2 - n^2) \over 2m(m + n)} = n(m -n).$$ By taking $n=1$ and $m=k + 1$ or alternatively $n = k$ and $m = k + 1$ we get $r = k$ for any integer $k$ (and of course the triangle has inradius $k$ even when $k$ is not an integer). For $r = 3$ we have $n = 1$ and $m = 4$ giving the triangle with sides 8, 15 and 17 or alternatively $n =3$, $m = 4$ in which case $a = 24$, $b = 7$ and $c = 25$. For $r = 4$ we can take $n = 4$, $m = 5$ which gives the Pythagorean triple $a = 40$, $b = 9$ and $c = 41$."
Sue's generalisation of this problem to isosceles triangles is given as a Further Inspiration.
You may also like
Baby Circle
A small circle fits between two touching circles so that all three circles touch each other and have a common tangent? What is the exact radius of the smallest circle?
Logosquares
Ten squares form regular rings either with adjacent or opposite vertices touching. Calculate the inner and outer radii of the rings that surround the squares.
Two Trees
Two trees 20 metres and 30 metres long, lean across a passageway between two vertical walls. They cross at a point 8 metres above the ground. What is the distance between the foot of the trees?