Overarch 2

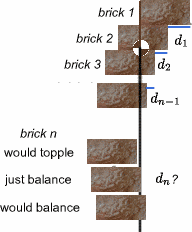We want to calculate the formula for the overhang $d_n$ of brick $n$ over brick $(n+1)$. (See the diagram). The idea is to imagine inserting brick $n$ under the existing pile of bricks 1, 2, 3...$(n-1)$ (numbering the bricks from the top) so that the centre of mass of bricks 1, 2, 3... $(n-1)$ will be exactly above the edge of brick $n$. You can treat the edge of brick $(n+1)$ as the fulcrum of a balance. The maximal arch will be created when there is a perfect balance on each edge.

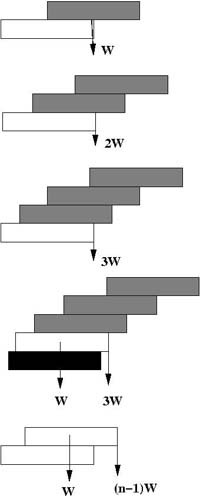If you calculate $d_1$, $d_2$,... you should find that \begin{eqnarray} d_1 &=& 1\\ d_2 &=& {1\over 2}\\ d_3 &=& {1\over 3}\\ \end{eqnarray} So it seems likely that $d_n = {1\over n}$. As the centre of mass of the stack of bricks above must be exactly over the edge of the next brick down, we take moments for the stack of $n$ bricks resting on the $(n+1)$st brick (counting the bricks from the top). We need the centre of mass of (n-1) bricks at distance $d_n$ from the fulcrum to balance 1 brick (the $n$th brick) at distance $(1 - d_n)$. Hence \begin{eqnarray} W(1 - d_n) &=& (n-1)Wd_n\\ d_n &=& {1\over n} \end{eqnarray} The total overhang $A_n$ for an arch containing $n + 1$ bricks is therefore $$ A_n = \sum_1^n 1/n $$

Alexander went on to say...

After some asking around, I was told there is no closed form for that. A small computer program that looks like this:

double overhang = 0;
double brickWidth = 20;
double maxOverhang = 100;
double numBricks = 0;
while (overhang < maxOverhang){
numBricks = numBricks+1;
overhang = overhang+brickWidth/(2*numBricks);
}

returns 12367 as the number of bricks needed to make an overhang of 1m, making its height 12367*10cm = 1,236.7m Since 1+1/2+1/3+...+1/n doesn't converge, you can make the overhang as big as you wish (I'm not gonna go into counting how much material for those bricks is needed and if there's enough of it in the universe :-) )