• Warm-up
• Try this next
• Think higher
• Read: mathematics
• Read: science
• Explore further

The wheels of a car, or a bicycle, run smoothly because they are separated from the axle of the wheel by a ring of ball bearings as illustrated below. Of course, the wheel turns smoothly because the ball bearings fit exactly between the hub of the wheel and the axle with no room to move about except, of course, to rotate. It is this rotation that keeps the friction to a minimum, and so makes the wheel turn smoothly.

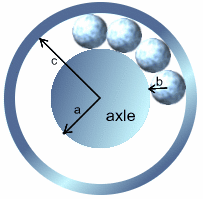
Suppose that $a$ is the radius of the axle, $b$ is the radius of each ball-bearing, and $c$ is the radius of the hub (see the figure).What are the ratios ${a\over b}$, ${b\over c}$ and ${c\over a}$ when there are exactly three ball-bearings? What are these ratios when there are exactly four ball-bearings? Try to explain why the number of ball bearings determines the ratio ${c\over a}$ exactly. Can you find a formula for ${c\over a}$ in terms of $n$ when there are exactly $n$ ball-bearings?