Ball Bearings
If a is the radius of the axle, b the radius of each ball-bearing, and c the radius of the hub, why does the number of ball bearings n determine the ratio c/a? Find a formula for c/a in terms of n.
Problem
The wheels of a car, or a bicycle, run smoothly because they are separated from the axle of the wheel by a ring of ball bearings as illustrated below. Of course, the wheel turns smoothly because the ball bearings fit exactly between the hub of the wheel and the axle with no room to move about except, of course, to rotate. It is this rotation that keeps the friction to a minimum, and so makes the wheel turn smoothly.
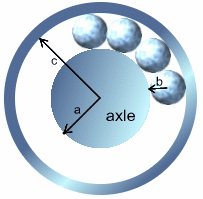
Suppose that $a$ is the radius of the axle, $b$ is the radius of each ball-bearing, and $c$ is the radius of the hub (see the figure).What are the ratios ${a\over b}$, ${b\over c}$ and ${c\over a}$ when there are exactly three ball-bearings? What are these ratios when there are exactly four ball-bearings? Try to explain why the number of ball bearings determines the ratio ${c\over a}$ exactly. Can you find a formula for ${c\over a}$ in terms of $n$ when there are exactly $n$ ball-bearings?
Getting Started
Can you find in the diagram a right angled triangle with angle ${\pi \over n}$?
Student Solutions
Sue Liu of Madras College, St Andrews sent an excellent solution to this question.
Suppose that $a$ is the radius of the axle, $b$ is the radius of each ball-bearing, and $c$ is the radius of the hub (see the figure).
The solution is based on the following figure.
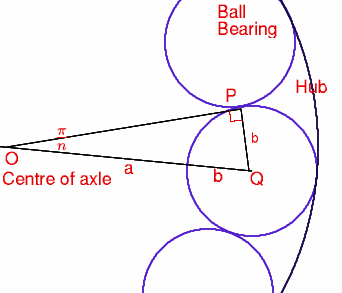
The angle subtended by each ball-bearing at the centre of the axle is $2\pi/n$, so that in the triangle $OPQ$ we have $$OQ= a+b, \quad PQ = b, \quad \angle POQ = \pi/n$$ and hence
- $$(a+b)\sin (\pi/n) = b.$$
We also know that
- $$c = OP' = OP +PP' = a+2b.$$
The rest of the solution is applying simple algebra to (1) and (2), and to simplify this we will (temporarily) write $s$ for $\sin (\pi/n)$. First, (1) gives $$ as = b(1-s).$$ Next, (2) gives $$c = a+2b = a + {2as\over 1-s} = a\left({1+s\over 1-s}\right),$$ so that, finally, we have $${a \over b} = \left({1 - \sin (\pi/n)\over \sin (\pi /n)}\right), \quad {b \over c} = \left({\sin (\pi/n)\over 1+\sin (\pi /n)}\right), \quad {c\over a} = \left({1+\sin (\pi/n)\over 1-\sin (\pi /n)}\right).$$ When there are 3 ballbearings, $n = 3$ and $\sin (\pi /3) = \sqrt 3 /2$. Hence$${a \over b}= {2\sqrt 3 \over 3} - 1, \quad {b \over c} = \sqrt 3(2 - \sqrt 3), \quad {c \over a} = 7 + 4\sqrt 3.$$ When there are 4 ballbearings, $n = 4$ and $\sin (\pi /4) = \sqrt 1 /\sqrt 2$. Hence $${a \over b}= \sqrt 2 - 1, \quad {b \over c} = \sqrt 2 - 1, \quad {c \over a} = 3 + 2\sqrt 2.$$ {\bf If $n=6$ then} $b = a$ and $c = 3a$. This is a very special case for suppose, in the general case, that the internal radius $c$ of the hub is an integer multiple of the radius $b$ of each ball-bearing. Then $c/b = N$, say, where $N$ is an integer, and this gives $$N\sin {\pi \over n} = 1+\sin {\pi\over n},$$ or $$\sin {\pi\over n} = {1\over N-1}.$$ Now it is known (although this is NOT an elementary result) that if $\sin x$ is rational, then $\sin x$ is $0$, $1/2$ or $1$. Thus we must have $${1\over N-1} = {1\over 2},$$ so that $N=3$. This means that $\sin (\pi/n) = 1/2$ so that $n=6$.
The same conclusion can be made if we know that in the general case the internal radius of the hub is an integer multiple of the radius of each ball-bearing.
Finally, as this same conclusion, namely $n=6$, can be drawn whenever one of the ratios $a/b$, $b/c$, $c/a$ are rational numbers and, as the case $n=6$ is not practical (many more ballbearings are needed) it follows that in all cases of, for example, bicycle wheels, these ratios are irrational. It therefore follows that it is impossible to manufacture a perfectly fitting set of ball-bearings.
