Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Shapely Pairs



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Shubhangee, Abheer, Hari, Ashlesha, Asma, Dia, Jamal, Aman, Adhrit, Akhil, Siddhanth, Harshad, Lasya, Kivisha, Ruhaan, Eshaan, Anirved, Saba and Ayaan from Ganit Kreeda, Vicharvatika in India and Ci Hui from Queensland Academy of Science Mathematics and Technology in Australia numbered the triangle cards, and noted what types of triangle would work for each card. This is the work from Ganit Kreeda:
Suppose instead of having the cards face down we have them all face up. If it's your turn first, how many possible pairs of cards are there that you could choose and win (that is, in how many ways could you choose a pair so that there is a triangle with both the properties)? Can you list all the possible pairs?
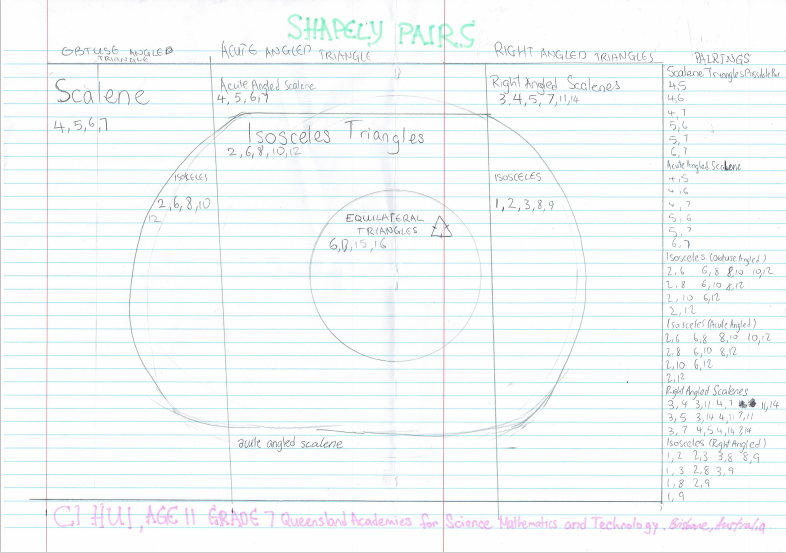
Ci Hui thought about this for each type of triangle. First, Ci Hui drew all the different types of triangle onto a Venn diagram, with a list of statements that apply to each type of triangle. Then, for each type of triangle, Ci Hui listed all of the pairs of cards for which you could draw that triangle. This is Ci Hui's work (click on the image to open a larger version):
Now suppose that you want to make a pile of cards so that no matter which two you pick, you can always draw a triangle with both those properties. How big could the pile be? Can you give an example?
Similar to Ci Hui's work, the students from Ganit Kreeda considered the different types of triangle. This is their work:
We grouped them from the type of triangles we got as:
1. Isosceles Right-angled Triangle - 6 cards
- Contains a right angle and has just 2 equal angles (1)
- Has just 2 equal sides (2)
- Contains a right angle (3)
- Has just 2 equal angles (8)
- Contains a right angle and has just 2 equal sides (9)
- Has only 1 line of symmetry (12)
2. Isosceles but not Right-angled Triangle - 5 cards
- Has just 2 equal sides (2)
- Does not contain a right angle (6)
- Has just 2 equal angles (8)
- Does not contain a right angle and has just 2 equal sides (10)
- Has only 1 line of symmetry (12)
3. Right-angled Scalene Triangle - 6 cards
- Contains a right angle (3)
- All its angles are of different sizes (4)
- Has no line of symmetry (5)
- All its sides are of different lengths (7)
- Contains a right angle and has all its sides of different lengths (14)
- Contains a right angle but does not have a line of symmetry (11)
4. Equilateral Triangle - 4 cards
- Has all its sides equal (13)
- Does not contain a right angle (6)
- Has three lines of symmetry (15)
- Has all its angles equal (16)
You may also like
Isosceles
Prove that a triangle with sides of length 5, 5 and 6 has the same area as a triangle with sides of length 5, 5 and 8. Find other pairs of non-congruent isosceles triangles which have equal areas.
Trice
ABCDEFGH is a 3 by 3 by 3 cube. Point P is 1/3 along AB (that is AP : PB = 1 : 2), point Q is 1/3 along GH and point R is 1/3 along ED. What is the area of the triangle PQR?