Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Dotty Relationship
Age 7 to 11
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Dotty Relationship
On the grid below, join the two blue dots, A and B, together with a straight line.Now join the green dots, C and D, with a straight line.
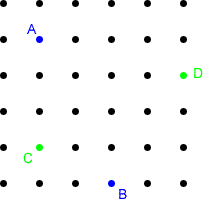
At what angle do the two lines cross?
Investigate the number of squares "along" and "down" from A to B compared with the number of squares "along" and "up" from C to D. What do you notice?
Using what you have found out, can you draw lines that are perpendicular (at $90^{\circ}$) to the lines drawn below?
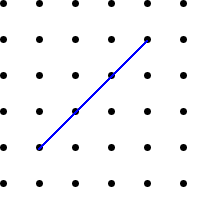
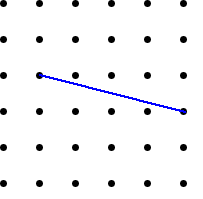
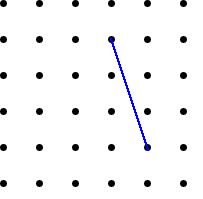
Is there only one solution each time?
Do the two lines have to be the same length? Why or why not?
Why do this problem?
This problem could be linked to coordinates. It could also form an introduction to vectors at a higher level. It is a powerful geometrical investigation. It has the potential to quickly lead to generalisations that pupils can apply in the second part of the question.Possible approach
The notion of "how long is a line?" would form an excellent discussion point in the plenary.Key questions
Possible extension
Possible support
You may also like
The Lily Pond
Freddie Frog visits as many of the leaves as he can on the way to see Sammy Snail but only visits each lily leaf once. Which is the best way for him to go?
A Cartesian Puzzle
Find the missing coordinates which will form these eight quadrilaterals. These coordinates themselves will then form a shape with rotational and line symmetry.
Transformation Tease
What are the coordinates of this shape after it has been transformed in the ways described? Compare these with the original coordinates. What do you notice about the numbers?