Keep Your Distance

An individual who is operating under the codename XYZ gave these correct examples:

Square - the $2$ different distances would be the SIDES (all same) and $2$ DIAGONALS (equal)



Parallelogram with angles $60$, $120$, $60$ and $120$ and the diagonal through the $120$ degrees angles is bisecting the angles. i.e. it ends up being a Rhombus with one of the diagonals equal to the sides.

Ellie offered the following as a solution:

The square and rhombus are given above. The kite would look like this:






Ray found one more:

 

And Ray and Kris found the last solution, based on four vertices of a regular pentagon (the red lines are the the length of the diagonals of a regular pentagon):

Well done to you all.

You may have thought initially that:

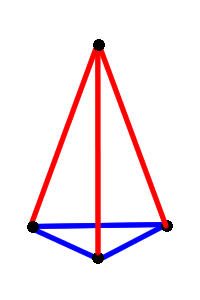
is a solution. Unfortunately it is not. Since if it was, then the blue triangle would be equilateral. Since all the lengths are relative, we can fix the length of one side and use this to find the lengths of the others:

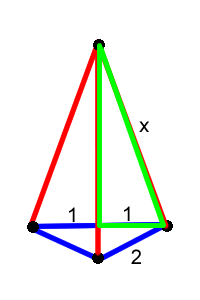
We can then use Pythagoras' Theorem on the bottom-right right-angled triangle to find that the missing length in the triangle is the square root $3$. But then the length of the unlabeled edge of the green right-angled triangle would be $x - \sqrt{3}$. We can now use Pythagoras' Theorem on this triangle:

\begin{eqnarray} x^2 &=& (x-\sqrt{3})^2+1 x^2 \\ &=& x^2-2\sqrt{3}x+3+1 \sqrt{3}\\ x &=& 2 x \\ &=& \frac{2}{\sqrt{3}}\\ &=& \frac{2}{3}\sqrt{3} \end{eqnarray}

But $x$ must be bigger than the square root of $3$, and so this solution is impossible!