Ladder and Cube

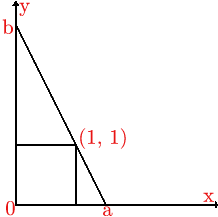This can be solved using a numerical search method (such as interval halving) to give the approximate solutions $b = 1.36$ and $3.76$ (to $2$ decimal places). These are the two possible heights of the top of the ladder. In each case, if one value is the height of the top of the ladder, the other value is the distance of the foot of the ladder from the wall.

Alternatively, the gradient is $-b/a = (1 - b)/(1 - 0)$, hence $ab = a + b $. Using the fact that $a^2 + b^2 = 16$ this gives $$(ab)^2 = (a + b)^2 = a^2 + 2ab + b^2 = 16 + 2ab.$$ Hence $$(ab)^2 - 2ab - 16 = 0.$$ Solving this equation gives $ab = 1 \pm \sqrt{17}$. As $a$ and $b$ are positive the solution here is $ab = 1 + \sqrt {17}$. We are looking for $a$ and $b$ and we know the sum $a + b$ and the product $ab$ are both equal to $1 + \sqrt{17}$. We can write down a quadratic equation with these roots and solve it. Hence $a$ and $b$ are the roots of $$x^2 - (1 + \sqrt{17})x + (1 + \sqrt{17}) = 0.$$

Solving this equation using the quadratic formula gives the values $3.7609$ and $1.3622$ (to $4$ decimal places). There are two solutions, one with the ladder at a steeper angle (it turns out to be approximately $70$ degrees) and the other at approximately $20$ degrees.

Yet another method uses numerical approximation. Taking the angle of the ladder with the ground to be $\theta$, then $a = 4 \cos \theta$ and $b = 4 \sin \theta$. Set up a spreadsheet or a program to evaluate $ab - (a + b)$ and use an interval halving method to find value of $\theta$ for which $ab - (a + b)$ is close enough to zero to give the values of $a$ and $b$ to sufficient accuracy.