Copyright © University of Cambridge. All rights reserved.
'Three Ball Line Up' printed from https://nrich.maths.org/
Show menu
We received some very well explained solutions to this problem. Many of you described how you used ordered your solutions so you knew you had all the solutions. We can call this 'working systematically'.
Jack from Tetherdown Primary sent his solution and his teacher said:
Jack worked out that there were six ways that three different coloured balls could land. At first, he stopped at four ways but then realised that if there were two ways of a red ball landing first, then there would be two ways
of a blue ball landing first and two ways of a green ball landing first.
Here is a picture of Jack's recording:
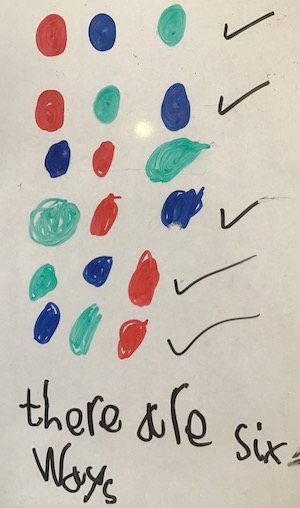
AT from ASB in the Netherlands used the same method:
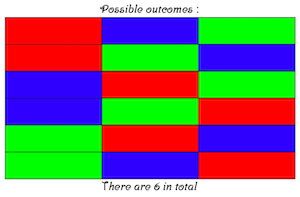
So, what I did was I first started with one colour, red and then I added blue and green. I did the same on the next one (still starting with red) but then green-blue.
So basically, I did the same for each of them and found six different outcomes...
It is easier if you just draw it on a piece of paper because then you can keep track of them easily!
Here is AT's drawing:
Pranaiv from Saint Bartholomews Primary School in Wolverhampton used a similar approach:

Thank you also to Roheena and Esther from Edgware Primary, who agreed with the six solutions.
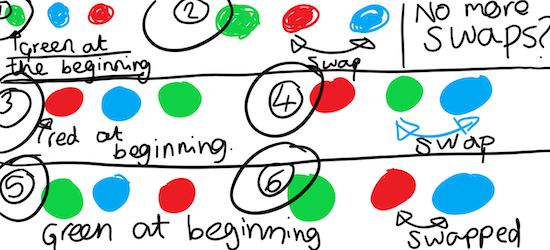
Maryam from the International Community School explained how she worked on the task, which again, was similar:
The balls can land in 6 different ways; each coloured ball (green, blue, red) can be in three different positions - front, middle and end. So if (for example) the green ball is at the front, the red and blue need to follow it, creating one solution. Then swapping the red and blue ball (with the green ball still at the front), we created the second solution. If we do the same with a turn for each coloured ball at the front, we get six possibilities in total.
Her recording is very clear:
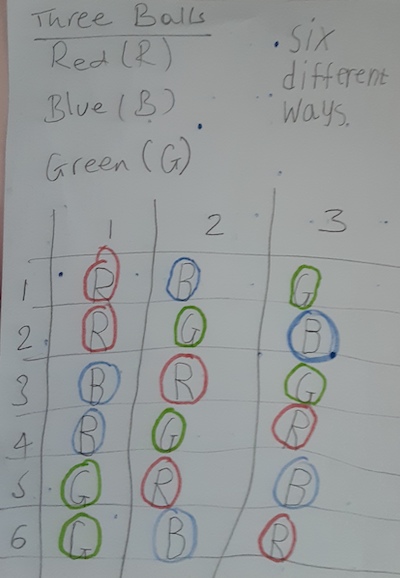
Mehetabel from Corpus Christi also organised her recording very clearly:
A pupil at St John the Baptist School in Wales shared this fantastic video explanation with us:
Thank you also to Charles from Clear Water Bay School in Hong Kong, Alex from Longsands School and Maria from Wimbledon High Junior School who all took the trouble to explain how they worked it out.
Aiste from VDU Rasos Gymnasium, Lithuania, wrote:
There are three balls and also three spaces for them.
So: _ _ _
We should put three different balls.
In the first place you can put all three balls. In the second place - 2 and at last in the third - 1.
So when we multiply these numbers and then will find the answer. 3x2x1 is 6.
I wonder why we multiply the numbers?