Copyright © University of Cambridge. All rights reserved.
'Triangles All Around' printed from https://nrich.maths.org/
Show menu
Chloe from Woodlea Junior School wrote:
To solve this problem I made all the dots connect with lines creating the maximum amount on triangles possible in each different circular pegboard.
On the 4 pegboard, I made 4 right angle triangles.
On the 6 pegboard, I made 18 triangles but I couldn't find out which triangles were there.
On the 8 pegboard, I made about 56 triangles, I may have counted wrong, but I can promise there were lots of triangles.
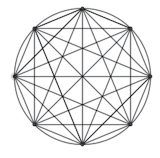
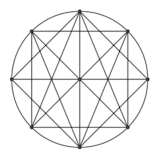
Georgia, also from Woodlea Junior School, wrote:
I knew that if you halve a diamond (or a square) it makes a triangle, so the first thing that I did was make a diamond on the circle. Then I made another diamond that was facing the other way round. By then, I already had about 15 triangles. After that, I turned on the centre point and started making lots of little triangles by connecting two lines in the centre so that they met in the middle and made a triangle shape. I did that over and over again, but each time I made sure that I wasn't ruining any of the other triangles unless when I did, it just split it into two smaller triangles. When I'd finished doing that, I couldn't do anymore because if I did, it would have made lots of the triangles turn into shapes that weren't triangles.
Nico from Toucan in Panama wrote:
I started by drawing squares inside the circle, then divided them by four. Each square gives you four triangle. Each peg should have 4 straight lines coming out from them.
Roberto also from Toucan in Panama said:
If you draw 4 straight lines out of each peg you make 4 triangles. In the end, you end up with 32 triangles out of each peg.
Thank you all. I wonder whether you thought about what makes one triangle different from another one... For example, on the four-peg board, Chloe says she created four triangles. Are they all different from each other?
Sam sent us her work on the problem, including the angles of all the triangles. Thank you Sam!
Can you see how she avoided counting any twice?
She first counted triangles with two corners on neighbouring pegs, then those two apart, and so on. She called two triangles the same if they had the same angles and not just if they used the same pegs. She explains this in a bit more detail below.
Here is her work:
First I labelled the points on the pegboard $ABCD$.
There are four possible triangles: $ABC$, $ABD$, $ACD$ and $BCD$. However these triangles are all the same shape (you can see this by rotating triangle $ABC$) so we could say that there is only one type of triangle that we can make.
This triangle has angles $90^\circ$, $45^\circ$ and $45^\circ$. I know this because if you draw a square around the points $ABCD$ and cut it in along the diagonal you get this triangle.
For the six point board, I again labelled the points as $ABCDEF$.
There are three possible triangles
$ABC$, with angles $120^\circ$, $30^\circ$ and $30^\circ$.
$ABD$, with angles $90^\circ$, $60^\circ$ and $30^\circ$.
$ACE$, with all angles $60^\circ$ (an equilateral triangle).
For the eight point board, I again labelled the pegs $ABCDEFGH$
There are five possible triangles
ABC, with angles $135^\circ$, $22.5^\circ$ and $22.5^\circ$.
ABD, with angles $112.5^\circ$, $22.5^\circ$ and $45^\circ$.
ABE, with angles $90^\circ$, $22.5^\circ$ and $67.5^\circ$.
ACE, with angles $90^\circ$, $45^\circ$ and $45^\circ$.
ACF, with angles $45^\circ$, $67.5^\circ$ and $67.5^\circ$.
Can you see how she worked out the angles in the triangles? Remember that the angles in a triangle add up to 180 degrees! You can divide the triangle (or the circle) into pieces whose angles you know to help you.
To solve this problem I made all the dots connect with lines creating the maximum amount on triangles possible in each different circular pegboard.
On the 4 pegboard, I made 4 right angle triangles.
On the 6 pegboard, I made 18 triangles but I couldn't find out which triangles were there.
On the 8 pegboard, I made about 56 triangles, I may have counted wrong, but I can promise there were lots of triangles.

Georgia, also from Woodlea Junior School, wrote:
I knew that if you halve a diamond (or a square) it makes a triangle, so the first thing that I did was make a diamond on the circle. Then I made another diamond that was facing the other way round. By then, I already had about 15 triangles. After that, I turned on the centre point and started making lots of little triangles by connecting two lines in the centre so that they met in the middle and made a triangle shape. I did that over and over again, but each time I made sure that I wasn't ruining any of the other triangles unless when I did, it just split it into two smaller triangles. When I'd finished doing that, I couldn't do anymore because if I did, it would have made lots of the triangles turn into shapes that weren't triangles.

Nico from Toucan in Panama wrote:
I started by drawing squares inside the circle, then divided them by four. Each square gives you four triangle. Each peg should have 4 straight lines coming out from them.
Roberto also from Toucan in Panama said:
If you draw 4 straight lines out of each peg you make 4 triangles. In the end, you end up with 32 triangles out of each peg.
Thank you all. I wonder whether you thought about what makes one triangle different from another one... For example, on the four-peg board, Chloe says she created four triangles. Are they all different from each other?
Sam sent us her work on the problem, including the angles of all the triangles. Thank you Sam!
Can you see how she avoided counting any twice?
She first counted triangles with two corners on neighbouring pegs, then those two apart, and so on. She called two triangles the same if they had the same angles and not just if they used the same pegs. She explains this in a bit more detail below.
Here is her work:
First I labelled the points on the pegboard $ABCD$.
There are four possible triangles: $ABC$, $ABD$, $ACD$ and $BCD$. However these triangles are all the same shape (you can see this by rotating triangle $ABC$) so we could say that there is only one type of triangle that we can make.
This triangle has angles $90^\circ$, $45^\circ$ and $45^\circ$. I know this because if you draw a square around the points $ABCD$ and cut it in along the diagonal you get this triangle.
For the six point board, I again labelled the points as $ABCDEF$.
There are three possible triangles
$ABC$, with angles $120^\circ$, $30^\circ$ and $30^\circ$.
$ABD$, with angles $90^\circ$, $60^\circ$ and $30^\circ$.
$ACE$, with all angles $60^\circ$ (an equilateral triangle).
For the eight point board, I again labelled the pegs $ABCDEFGH$
There are five possible triangles
ABC, with angles $135^\circ$, $22.5^\circ$ and $22.5^\circ$.
ABD, with angles $112.5^\circ$, $22.5^\circ$ and $45^\circ$.
ABE, with angles $90^\circ$, $22.5^\circ$ and $67.5^\circ$.
ACE, with angles $90^\circ$, $45^\circ$ and $45^\circ$.
ACF, with angles $45^\circ$, $67.5^\circ$ and $67.5^\circ$.
Can you see how she worked out the angles in the triangles? Remember that the angles in a triangle add up to 180 degrees! You can divide the triangle (or the circle) into pieces whose angles you know to help you.