Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Triangles in Circles
Age 11 to 14
Challenge Level 





- Problem
- Student Solutions
- Teachers' Resources
Why do this problem ?
This problem challenges students to apply what they know about angles in triangles. The nine-point circle allows students to concentrate on the geometrical structure while keeping the arithmetic reasonably straightforward.It offers a good preparation for the problems Subtended angles, Right angles, and Cyclic Quadrilaterals, which lead to proofs of circle theorems.
Teachers may find the article Angle Measurement: an Opportunity for Equity of interest.
Possible approach
"How many different triangles can you make which consist of the centre point and two of the points on the edge? "
"Can you find all the angles of the triangles?"
At some stage students will want to know what makes triangles "different". This is a good opportunity to talk about congruence.
After a short time bring the class together to discuss how they calculated the angles.
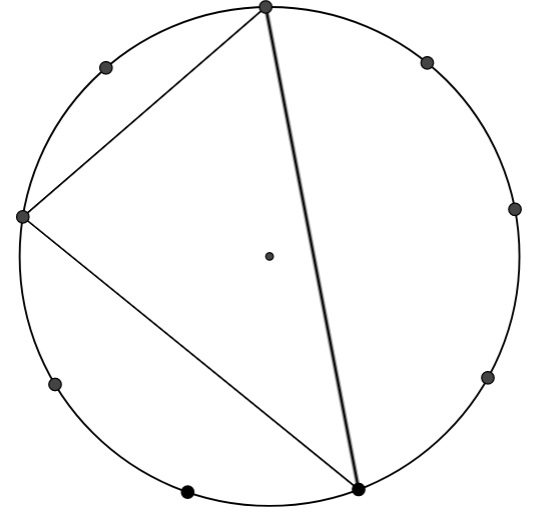
Next, draw a triangle with three vertices on the edge of the circle which encloses the centre point, such as the one illustrated here.
"Using what you already know, can you find all the angles of this triangle?"
After a few minutes, bring the class together to discuss what strategies they have used. It may be necessary to draw in the isosceles triangles to help students to relate this problem to what they have already found out.
Once they have a strategy, invite them to find as many different triangles as they can, and work out the angles. At some stage, you may need to discuss how to cope with triangles that do not enclose the centre.
Key questions
What do you know that might be useful?Are there any extra lines you can draw, to help make the problem more like something you've seen before?