Total Totality
Age
11 to 14
Challenge level
Is it possible to arrange the numbers 1-6 on the nodes of this diagram, so that all the sums between numbers on adjacent nodes are different?
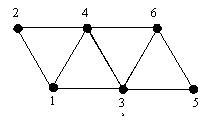
Problem
This network has nine edges which meet at six nodes. The numbers $1$, $2$, $3$, $4$, $5$, $6$ are placed at the nodes, with a different number at each node. Is it possible to do this so that the sum of the $2$ numbers at the ends of an edge is different for each edge?
Image
Either show a way of doing this, or prove that it is impossible.
More Total Totality is a follow-up short problem to this one.
More Total Totality is a follow-up short problem to this one.
If you liked this problem, here is an NRICH task which challenges you to use similar mathematical ideas.
Student Solutions
The task is possible to do as shown.
Image
