Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Parallelogram in the Middle
Age 11 to 14
ShortChallenge Level 





- Problem
- Solutions
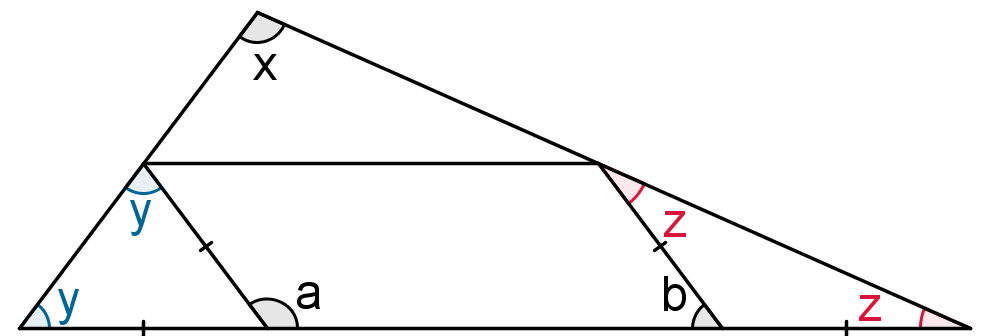
The two angles marked $y ^{\circ}$ are equal because they are in an isosceles triangle. For the same reason, the angles $z^{\circ}$are equal. Since an exterior angle of a triangle is the sum of the two interior and opposite angles, it follows that $a=2y$ and $b=2z$. Now $a^{\circ}+ b^{\circ} = 180^{\circ}$ since they are the base angles of a parallelogram. So $2y + 2z = 180$ giving $y+z=90$. But, from the angle sum of a triangle $x+y+z=180$; hence $x =90$.
This problem is taken from the UKMT Mathematical Challenges.
You can find more short problems, arranged by curriculum topic, in our short problems collection.
You may also like
Arclets Explained
This article gives an wonderful insight into students working on the Arclets problem that first appeared in the Sept 2002 edition of the NRICH website.
Bow Tie
Show how this pentagonal tile can be used to tile the plane and describe the transformations which map this pentagon to its images in the tiling.