Multiplicaton Square printable sheet - problem
Multiplication Square printable sheet - grid

Take a look at the multiplication square below:




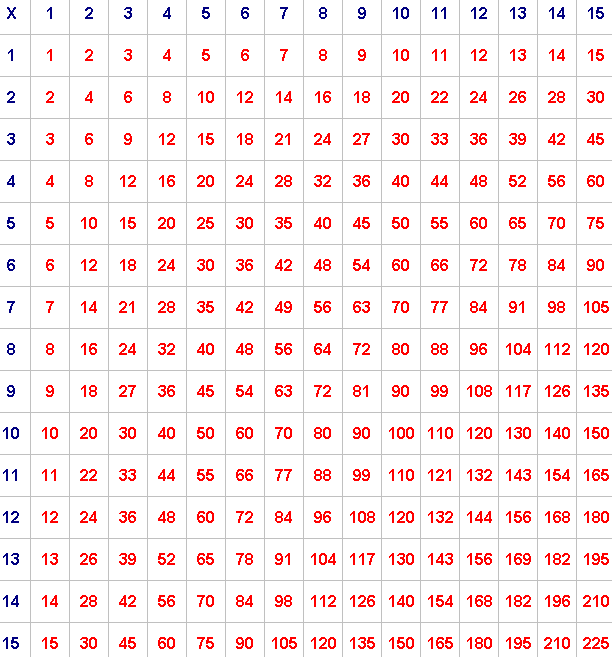
Pick any 2 by 2 square and add the numbers on each diagonal.
For example, if you take:

the numbers along one diagonal add up to $77$ ($32 + 45$)
and the numbers along the other diagonal add up to $76$ ($36 + 40$).

Try a few more examples.
What do you notice?
Can you show (prove) that this will always be true?

Now pick any 3 by 3 square and add the numbers on each diagonal.
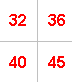
For example, if you take:

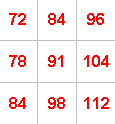
the numbers along one diagonal add up to $275$ ($72 + 91 + 112$)
and the numbers along the other diagonal add up to $271$ ($84 + 91 + 96$).

Try a few more examples.
What do you notice this time?
Can you show (prove) that this will always be true?

Now pick any 4 by 4 square and add the numbers on each diagonal.
For example, if you take:

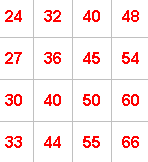
the numbers along one diagonal add up to $176$ ($24 + 36 + 50 + 66$)
and the numbers along the other diagonal add up to $166$ ($33 + 40 + 45 + 48$).

Try a few more examples.
What do you notice now?
Can you show (prove) that this will always be true?

Can you predict what will happen if you pick a 5 by 5 square, a 6 by 6 square ... an n by n square, and add the numbers on each diagonal?

Can you prove your prediction?

Click here for a poster of this problem.