Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Pentagonal
Age 14 to 16
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Laura sent us her work on this problem. Well done, Laura!

Let the square have side length $l$. Then its perimeter is $4l$. Also, we can see from the diagram above that the sum of the distances from the point to the top and bottom sides is $l$, and similarly the sum of the distances from the point to the left and right sides is $l$, so the total sum of the distances is $2l=\frac{1}{2}\times 4l$, which is constant and half of the perimeter.
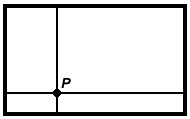
Let the rectangle have height $h$ and width $w$. Then its perimeter is $2(h+w)$. This is very similar to the square. Here the sum of the distances from $P$ to the top and bottom sides is $h$, and the sum of the distances from $P$ to the right and left sides is $w$, so the total sum of the distances is $h+w=\frac{1}{2}\times 2(h+w)$ is constant, and again is half of
the perimeter.
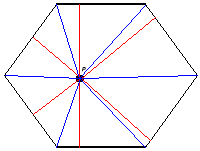
This hexagon isn't regular, but it is equilateral (all its sides have the same length, $l$, say). I've drawn on the perpendicular lines (in red) from $P$ to the sides, and have also divided the hexagon into six triangles (in blue), each with base $l$ and height the distance from that side to the point. The area of the hexagon can therefore be written as
$\frac{1}{2}(\textrm{sum of the heights})\times l$. Since this is constant, so is the sum of the heights.\par In the same way, the sum of the distances in an equilateral pentagon is constant.
You may also like
A Scale for the Solar System
The Earth is further from the Sun than Venus, but how much further? Twice as far? Ten times?
Swimmers
Swimmers in opposite directions cross at 20m and at 30m from each end of a swimming pool. How long is the pool ?