 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Diagonal Sums



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Diagonal Sums
Here is a $100$ square with some of the numbers shaded:
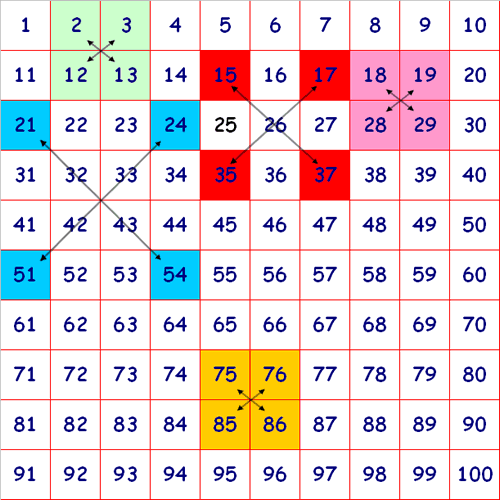
Look at the green square which contains the numbers $2, 3, 12$ and $13$.
What is the sum of the numbers that are diagonally opposite each other?
Do you notice anything?
Look at the pink square.
Does the same thing happen?
What about the yellow square?
You could try with other squares which have four numbers in them.
Why does this happen?
Look at the squares shaded red. They form the corners of a large $3$ by $3$ square.
If you add the numbers diagonally opposite each other, what happens?
Why?
What happens for squares of different sizes?
You may like to print off this 100 square to try out some different squares of numbers.
Why do this problem?
This problem demonstrates the power of the 100 square in helping pupils to recognise number properties and in beginning to reason carefully. The latter, at this level, can be considered as a form of proof. It also gives an opportunity for some to use an intuitive form of algebra.
Possible approach
With all the children together looking at a large display of a 100 square and then choosing the 2, 3, 12, 13 square (without the multiplying arrows) and sharing all the observations that the pupils make. Some of these may be at a simple straightforward level; "the units of the ones above are the same", "the total is 30".
When many observations have been made the idea of multiplying opposite corners could be suggested - if it has not already occurred.
This is now beginning to move into slightly harder realms and it may (according to the abilities of the pupils) be a good time to give out copies of the activity.
Key questions
If pupils have, in the introduction given a total for the four numbers it would be good to ask them how they added up the four numbers.
When the pupils are working on the activity it would be good to ask what they are noticing.
It may be appropriate to ask the to explain further how they know the things they have observed.
Possible extension
Ask for a proof that their observations will always happen?
Can they predict what to do for a 6 by 6 square?
Thank you to Mark Burdass, a teacher at Harlands Primary School in Haywards Heath, who suggested the following further extension tasks:
- What about the corners of an oblong? What happens when you add these?
- What about the corners of a tilted square? What happens when you add these?
- Can you find any other quadrilaterals (such as parallelograms, rhombuses, trapeziums or kites) that behave in the same way?
Possible support
The printable version of the 100 square might be useful for children to try out a variety of diagonal sums.