"The mathematician's patterns, like the painter's or the poet's, must be beautiful; the ideas, like the colours or the words, must fit together in a harmonious way. Beauty is the first test: there is no permanent place in the world for ugly mathematics." G.H Hardy

"In mathematics, if a pattern occurs we can go on to ask 'Why does it occur?' 'What does it signify?' and we can find answers to these questions." W.W.Sawyer

Mathematics is full of beautiful patterns, of explanations always there if we can only find them, and of occurances of the same idea in many different contexts. There is a reason for everything in mathematics and we should try to avoid taking anything for granted without an explanation. Proof in mathematics involves finding answers to questions like 'Why does this pattern occur?' and 'What does is signify?'.

This article poses such questions in relation to a few of the properties of the Golden Ratio and Fibonacci sequences and proves these properties. The reader needs to be happy with the language of algebra and curious about why mathematical results happen as they do.

While the article introduces some powerful mathematical ideas widely used in higher mathematics, no knowledge is needed beyond the level of mathematics usually met by the age of sixteen in school. The article starts with a numerical method to find the value of the Golden Ratio, it explains how the cellular automata introduced in the problem Sheep Talk produces the Fibonacci sequence and the Golden Ratio, and finally it builds a sequence of continued fractions and shows how this sequence converges to the Golden Ratio. Two by two matrices are used to solve simultaneous linear equations but prior knowledge of matrices is not necessary.

An iterative method to give a numerical value of the Golden Ratio $\phi$ is suggested by the formula which defines the Golden Ratio, namely $$\phi = 1 + {1\over \phi}.$$ Take the initial approximation $\phi_0 = 1$. To get the next approximation in the sequence $\phi_{n+1}$ just add 1 to the reciprocal of the previous approximation $\phi_n$. The formula is $$\phi_{n+1} = 1 + {1\over \phi_n}, \quad \phi_0=1.$$ The first few terms of this sequence are: $$1,\ 2,\ 1.5,\ 1.\overline 6,\ 1.6,\ 1.625,\ 1.6154...$$ and if you calculate a few more terms of this sequence you will find that it rapidly converges to $\phi$ giving the value to six significant figures, 1.61803, in just thirteen steps and giving more accuracy with more steps.

What does this have to do with the Fibonacci sequence? Well, this is a sequence of fractions, so suppose $$\phi_n = {b_n\over a_n }.$$ Then $$\phi_{n+1} = {b_{n+1}\over a_{n+1}}= 1 + {a_n\over b_n} = {b_n + a_n \over b_n}.$$ This is equivalent to $$\eqalign{ b_{n+1} &= b_n+a_n \cr a_{n+1} &= b_n .}$$ The most convenient way to write down this pair of simultaneous equations, and to calculate the terms of the sequence generated by the iterative process described here, is to use two by two matrices. The advantage is that multiplication by a matrix computes two sequences of terms in one operation. What is more, graphical calculators will do this for you automatically. If you have to multiply by the same matrix again and again and again ... , that is by a power of the matrix, then the calculator will work out the power for and you can calculate many steps of the iteration in one go. Readers can check the rule for multiplying matrices in the Thesaurus. $$\pmatrix {b_{n+1}\cr a_{n+1}}= \pmatrix {1 & 1 \cr 1 & 0}\pmatrix {b_n \cr a_n}$$ Now carrying out the iteration has become a matter of multiplying by a matrix. We can do this again:

$$\pmatrix {b_{n+1}\cr a_{n+1}}= \pmatrix {1 & 1 \cr 1 & 0} \pmatrix {1 & 1 \cr 1 & 0}\pmatrix {b_{n-1} \cr a_{n-1}}=\pmatrix {1 & 1 \cr 1 & 0}^2 \pmatrix {b_{n-1} \cr a_{n-1}} $$

and we can keep repeating this over and over again to give: $$\pmatrix {b_{n+1}\cr a_{n+1}}=\pmatrix {1 & 1 \cr 1 & 0}^n \pmatrix {b_1 \cr a_1} $$ The cellular automaton in the problem \href{http://nrich.maths.org/public/viewer.php?obj_id=2683'??=index} {Sheep Talk} produces a sequence of words containing only the two letters A and B. The rule is that the first word is A and to get the next word in the sequence you change every A in the word before it to B and every B to AB. The first few words are: A, B, AB, BAB, ABBAB,... . Write a few more words for yourself and count the number of A's and B's in each word. Writing $a_n$ and $b_n$ for the number of A's and B's in the $nth$ word, the generating rule becomes: $$\eqalign{ b_{n+1} &= b_n+a_n \cr a_{n+1} &= b_n .}$$ This is the same pair of sequences used earlier in the iterative process. Substituting $b_{n-1}$ for $a_n$ in the second of these formulae gives $b_{n+1}=b_n+b_{n-1}$ showing that the sequence of B's is the Fibonacci sequence starting with 0, 1 ... and likewise it can easily be shown that the sequence of A's is the Fibonacci sequence starting with 1, 0,... Thus we have found that the ratio of successive terms of a Fibonacci sequence $a_{n+1}/a_n$,which is equal to $b_n/a_n$, converges to the Golden Ratio.

How does this tie in with continued fractions? Well let's review how we set up the iteration $\phi_{n+1}= 1 + 1/\phi_n$. We started with $\phi_0=1$. Now substituting the successive values of $\phi_n$ into the iteration formula be build up a sequence of continued fractions: $$\eqalign{ \phi_0 &=1 \cr \phi_1 &= 1 + {1 \over 1} \cr \phi_2 &= 1 + {1\over \phi _1} = 1+ {1\over\displaystyle 1+ { 1 \over \displaystyle 1}}\cr \phi_3 &= 1 + {1\over \phi_2} = 1+ {1\over\displaystyle 1+ { 1 \over \displaystyle 1+ { 1\over 1}}}\cr \phi_4 &= 1 + {1\over \phi_3} = 1+ {1\over\displaystyle 1+ {1\over\displaystyle 1+ {1 \over \displaystyle 1+ {1\over 1}}} },...} $$ Clearly we can write more and more terms of this sequence, and the continued fractions become longer but the whole sequence is described by the mapping formula $$\phi_{n+1} = 1 + {1\over \phi_n} = {\phi_n + 1 \over \phi_n}.$$

To show that this sequence of mappings must converge consider the graphs of $y=x$ and $y=1+1/x$. If the mapping $x_{n+1}= 1 + 1/x_n$ tends to a limit $\phi$ then, for very large $n$, we must be able to replace both $x_{n+1}$ and $x_n$ by $\phi$ which is shown on the graph at the intersection of $y=x$ and $y=1 +1/x$.

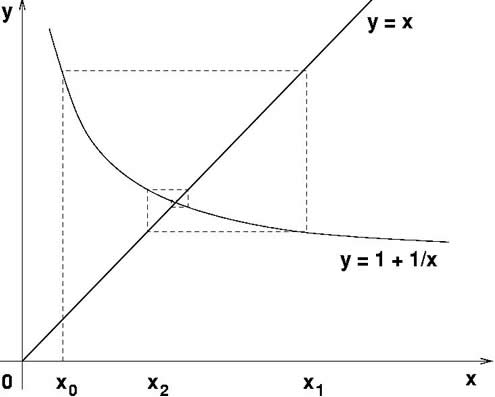
Taking the first approximation $x_0$ , draw a vertical line through $x=x_0$ to meet the graph of $y=x+1/x$ where the $y$ value gives the next approximation $x_1$. Next draw a horizontal line through this point to hit the graph of $y=x$ at $(x_1, x_1)$. From this point draw a vertical line down to meet the graph of $y=1 + 1/x$ at $(x_1, x_2)$. To locate the next approximation draw a horizontal line through this point to meet the graph of $y=x$ at $(x_2, x_2)$. Continuing in this way you form the 'cobweb' diagram shown and get closer and closer approximations to the Golden Ratio $\phi$.

For those who want to explore more of the related patterns and mathematical results there are many challenges and articles on this website alone and thousands elsewhere on the web to be found using any search engine.