Copyright © University of Cambridge. All rights reserved.
'Triangles Within Squares' printed from https://nrich.maths.org/
Show menu
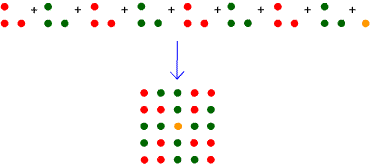
The diagram above shows that: $$ 8 \times T_2 + 1 = 25 = 5^2$$
Use a similar method to help you verify that: $$ 8 \times T_3 + 1 = 49 = 7^2$$ Can you generalise this result?
Can you find a rule in terms of $ T_n $ and a related square number?
Can you find a similar rule involving square numbers for $T_{n}, T_{n+2}$ and several copies of $T_{n+1}$?