You may also like
Odd Differences
The diagram illustrates the formula: 1 + 3 + 5 + ... + (2n - 1) = n² Use the diagram to show that any odd number is the difference of two squares.
Triangular Triples
Show that 8778, 10296 and 13530 are three triangular numbers and that they form a Pythagorean triple.
Iff
Take a triangular number, multiply it by 8 and add 1. What is special about your answer? Can you prove it?
Age 14 to 16
Challenge Level
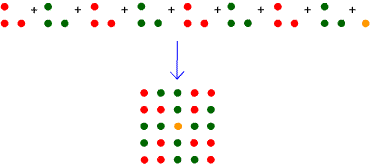
The diagram above shows that: $$ 8 \times T_2 + 1 = 25 = 5^2$$
Use a similar method to help you verify that: $$ 8 \times T_3 + 1 = 49 = 7^2$$ Can you generalise this result?
Can you find a rule in terms of $ T_n $ and a related square number?
Can you find a similar rule involving square numbers for $T_{n}, T_{n+2}$ and several copies of $T_{n+1}$?
Copyright © 1997 - 2023. University of Cambridge.
All rights reserved.
NRICH is part of the family of activities in the Millennium Mathematics Project.
NRICH is part of the family of activities in the Millennium Mathematics Project.