Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Late Again
Age 5 to 7
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Late Again
Here is a picture of Moira's school which has a paved playground at the front:
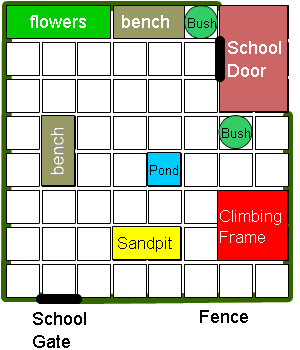
If Moira was sitting on the bench nearest the school gate, to get to the climbing frame she could:
Go forward $2$ squares to the pond.
Turn to the right and go $1$ square forward.
Turn to the left and go $2$ squares forward.
This morning, Moira is late for school.
What is the shortest route she can take from the school gate to the school door?
Is there more than one way she could go?
Why do this problem?
This problem introduces children to the language involved in describing position and direction. It could be done in a practical context and adapted to suit your playground.
It would be useful to project the plan onto a screen for the children to see and you could give pairs a copy of it on paper. This sheet contains two plans.
Key questions
Which direction might you go in first?
Try and describe any route.
Can you make it shorter?
How will you know which routes you have tried?