Cuisenaire Counting

Jack, Alice, Phoebe, Eva and Holly from Georgeham C of E School explained their findings:

We did all the 1s.
 
Then we did one 2 block on the right filling in the spaces with 1s.
We moved the 2 block over a square, filled that with 1s.
Then we moved the 2 block over again and filled the space with 1s.
We moved the 2 block for the last time with 1s in the spaces.

The pattern for two 2 blocks is... there's a single white square on the left with two 2 blocks on the right.
There's another with the single white square in between the two 2 blocks.
The third is the single white square on the right with the two 2 blocks on the left.
 

So, I think that makes eight ways in total.  I love the way you have done this in a careful order.  As Chelsea from Templars Primary said:

... the trick is to work systematically ...

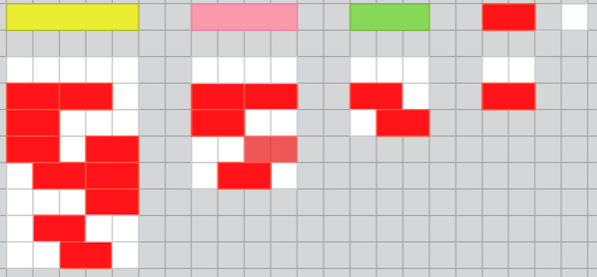
Laura sent in her solution as pictures copied from the interactivity, which is very helpful - thank you, Laura.

Here is her solution to the first challenge which we can compare with the solution from Georgeham:

Laura's pictures are in a slightly different order to the children from Georgeham's.  I wonder which you think is more systematic?  

Here Laura shows the thirteen different ways to make the green rod using reds and whites:

Would you have done them in the same order?  Why or why not?