 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Published 2011
Pythagoras
Pythagoras (say "pie-thag-or-as") of Samos was a Greek philosopher who lived from about 580 BC to about 500 BC. He made important developments in mathematics, astronomy, and the theory of music.
Pythagoras spent much of his life studying mathematics and formed a special school where members followed strict rules, such as never eating meat. Pythagoras believed that everything in the world could be explained by numbers and his school worked hard to try to learn enough about numbers to be able to understand the universe.

This is someone's idea of what Pythagorus might have looked like
Some of the things they believed about numbers seem odd to us now. For example, numbers were thought to have their own special nature. Pythagoreans thought numbers were male or female, ugly or beautiful, or had a special meaning.
Other ideas they worked on are things you still learn about in school and that mathematicians still use. Some of these are:


The school of Pythagoras also studied shapes and were particularly interested in triangles. One theorem (a statement of an idea) they worked on was:
The sum of the angles of a triangle is equal to two right angles .
This means that if you take any triangle, tear off the corners and fit them together like a puzzle, you will make a straight line (that is the same as two right-angles).
Perhaps the most famous theorem in the world is known as Pythagoras' theorem. It is thought that it was known to the Babylonians 1000 years earlier but Pythagoras may have been the first to prove it.
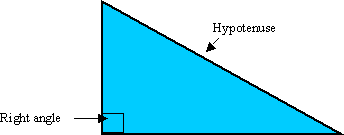
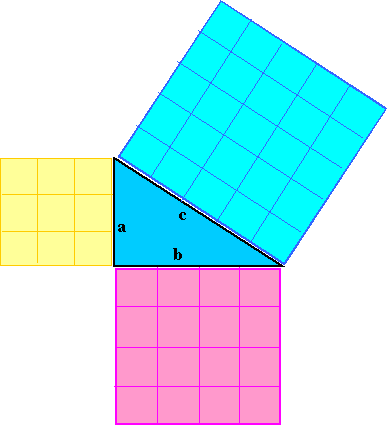
The theorem is: for a right-angled triangle the square on the hypotenuse is equal to the sum of the squares on the other two sides.
'Hypotenuse' is the name given to the side that is opposite the right angle.
If you would like to find out more about Pythagoras visit the St Andrews History of Mathematics website.