 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Just Opposite



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Just using coordinates and the clue in the original diagram there is a short and sweet solution sent in by Jo from Leeds.
By concentrating on the geometry, she made the algebra very simple. With the clue that $p-q = a-c$ and $p+q=b-d$ she was able to find the area of the square $ABCD$:
The inner square would have a side of $6-3 =3$.
The area of the tilted square is therefore $5 \times 5 - \frac{(5 \times 5)-(3 \times 3)}{2} =17 $ sq units and this can be generalised.
In the algebraic case.
Area $= (b-d)^2- \frac{((b-d)^2- (a-c)^2)}{2} $
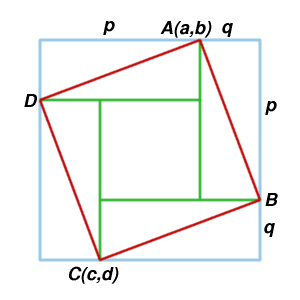
Michael Gray from Madras College solved the first part using vectors.
The midpoint of the square is given by $M=((a+c)/2, (b+d)/2)$. Hence
You may also like
Fitting In
The largest square which fits into a circle is ABCD and EFGH is a square with G and H on the line CD and E and F on the circumference of the circle. Show that AB = 5EF. Similarly the largest equilateral triangle which fits into a circle is LMN and PQR is an equilateral triangle with P and Q on the line LM and R on the circumference of the circle. Show that LM = 3PQ
Zig Zag
Four identical right angled triangles are drawn on the sides of a square. Two face out, two face in. Why do the four vertices marked with dots lie on one line?