The solution to this tough nut was submitted by Ray who does not reveal his school.

By Pythagoras' Theorem: $$|AB|=\sqrt 3,\ |BC|=\sqrt 2,\ |AC|=\sqrt 5,\ |BD|=\sqrt 5,\ |AD|=\sqrt{10}.$$ As $|AB|^2 + |BC|^2 = |AC|^2$ it follows, by the converse of Pythagoras' Theorem, that $\angle ABC = 90^o$.

Using the cosine rule: $|AD|^2 = |AB|^2 + |BD|^2 - 2|AB||BD|\cos B.$ So $$\cos B= {-1\over \sqrt{15}}$$ and $\angle ABD = 105$ degrees to the nearest degree.

The challenge was to find more than one method so the second method uses geometry and vectors.

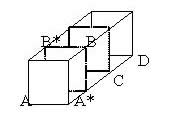Triangle $A^*BC$ is a right angled isosceles triangle and $A^*B$ is perpendicular to $BC$.The line $B^*B$ is perpendicular to the plane $A^*BDC$ so it is perpendicular to $BC$. As the two line $A^*B$ and $B^*B$ are perpendicular to $BC$ the whole plane $AB^*BA^*$ is perpendicular to $BC$. Hence $AB$ is perpendicular to $BC$.