Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Degree Ceremony



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
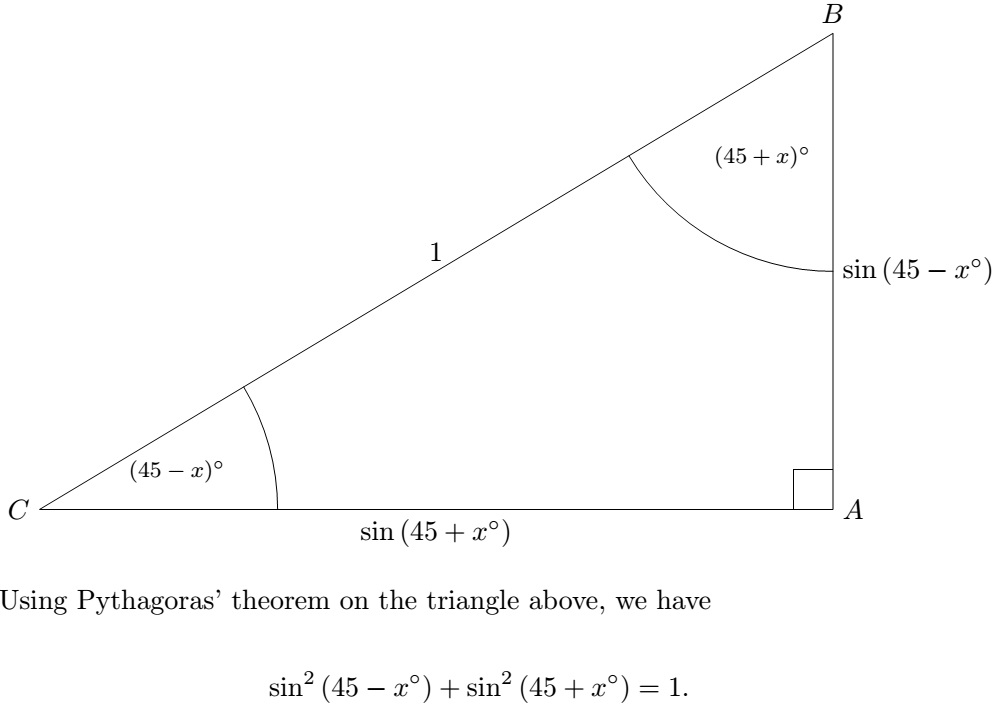
Dylan from Brooke Weston and Soumya from King's Maths School in the UK used diagrams and two sines to solve the problem. Here is Dylan's work:
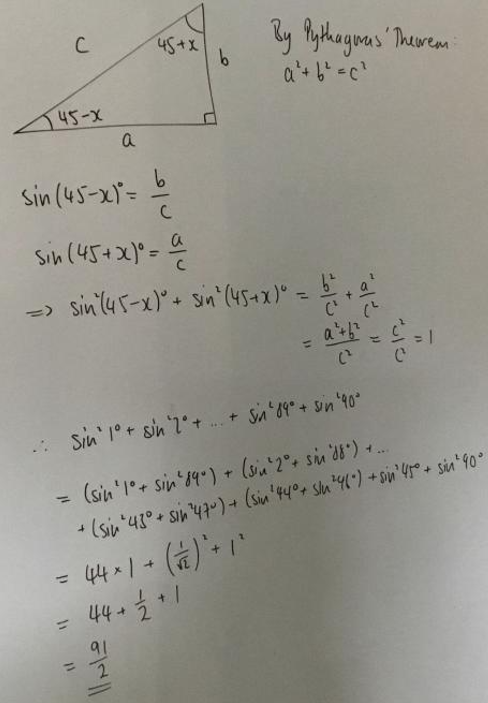
Soumya used a slightly different diagram, but the rest of the working was the same. Here is Soumya's diagram and the first line of Soumya's working:
Joshua, Gautham and Nishad used sines and cosines with another identity. This is Nishad's work:
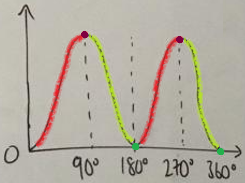
For the sum up to $\sin^2360^\circ$, Dylan and Joshua used graphs and symmetry. This is Joshua's work:
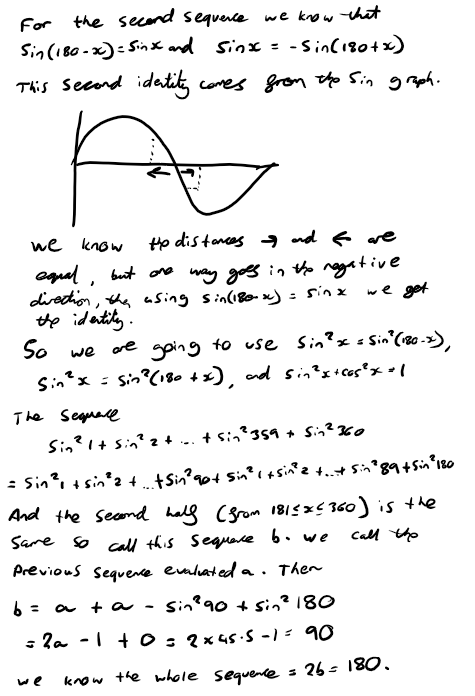
Dylan used a more graphical method which includes graph transformations. This is Dylan's work:
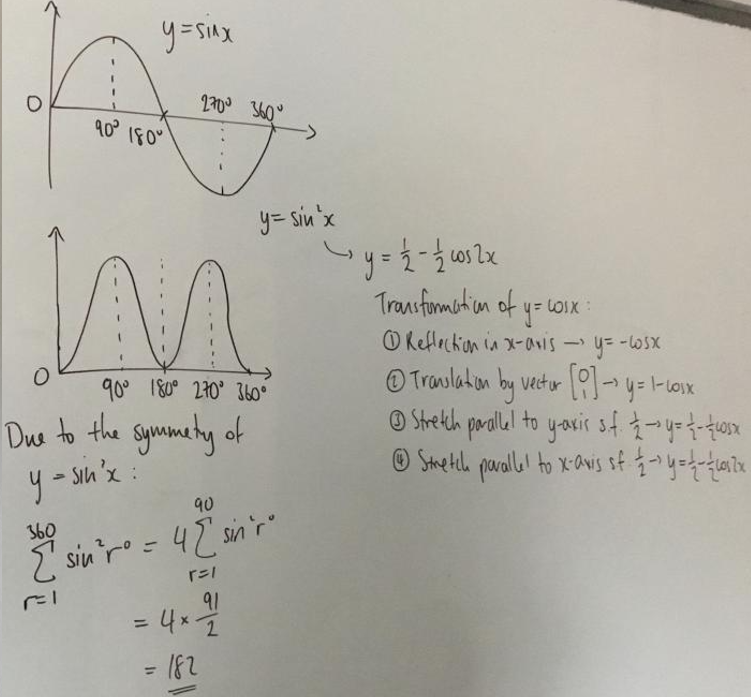
Note that Dylan's answer is slightly wrong. Can you use this diagram to see why?
Gautham and Soumya showed more terms in their working, so Dylan's lost terms are clearer. Here is Gautham's work (click on the image to see a larger version):
Soumya used sigma notation to express the same thing (click on the image to see a larger version):