Octa-flower

Stage: 5 Challenge Level:

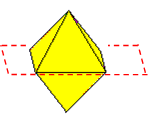
Think in 3D of a flower made from regular octahedra with the vertices of the octahedra meeting at a point and faces in contact. How many octahedra can be joined together in this way around one centre?

Here is a solution from Andrei of Tudor Vianu National College, Bucharest, Romania.

First, I observe that the octahedron is symmetrical about a plane that passes through the 4 coplanar vertices (see figure), so for the problem I may take into account only a pyramid.

I shall calculate angle $MVN$.

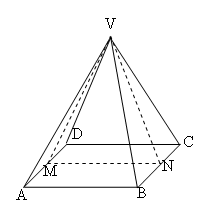
As all exterior sides have equal lengths, without loss of generality I may assume $AB = 1$. In this case $VN$ is the height of equilateral triangle $VBC$, so it has a length of $\sqrt 3 /2$. $MN$ is equal to $AB$, having a length of 1.

To calculate angle $MVN$, I shall calculate its sine.

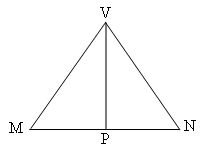
$$\eqalign { \sin MVN &= 2\sin{{\angle MVN \over 2}}\cos{{\angle MVN \over 2}} \cr &= 2{MP\over MV}{VP\over MV}\cr &= 2. {1/2 \over \sqrt 3/2}.{\sqrt 2/2 \over \sqrt 3/2}\cr &= {2\sqrt 2 \over 3} }$$

The angle at $MVN$ (to 3 decimal places) is $$\sin^{-1}2\sqrt 2/3 = 70.529^o .$$ Alternatively you could calculate this angle as $$2\sin^{-1}1/\sqrt 3 = 70.529^o .$$ The number of octahedra is $360/70.529 = 5.1$.

So 5 tetrahedra could be joined together in this way.

Cosine. Angles at a point/on a line. Symmetry. Octahedra. Sine. Cross sections. Graph sketching. Asymptotes. Complex numbers. Trigonometric identities.