Copyright © University of Cambridge. All rights reserved.
'Golden Construction' printed from https://nrich.maths.org/
Show menu
In this problem you start with a square, construct a golden rectangle and calculate the value of the golden ratio.
When you cut a square off a golden rectangle you are left with another rectangle whose sides are in the same ratio. In the diagram below, if you remove the orange square from rectangle $AEFD$, you are left with the yellow rectangle whose sides are in the same ratio as $AEFD$.
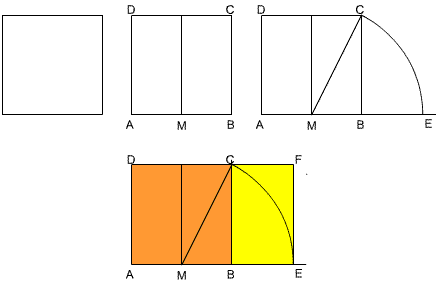
(1) Follow the instructions for drawing the rectangle $AEFD$. You can make the most accurate drawing by using a ruler and compasses. Draw a square $ABCD$ of side length 10 cm. Bisect $AB$ at $M$ and draw an arc of radius $MC$ to meet $AB$ produced at $E$. If you prefer you can just measure $MC$ and mark $E$ on $AB$ so that $ME=MC$. Draw $EF$ perpendicular to $AB$ to meet $DC$ produced at $F$.
Measure $AE$ and $BE$. From your measurements calculate the ratios $AE$/$AD$ and $BC/BE$. What do you notice?
(2) Calculate the exact lengths of $MC$, $AE$ and $BE$. Calculate the exact value of the ratios $AE$/$AD$ and $BC$/$BE$ and prove that they are equal. [Note: To get exact values you must work with surds and you will not be able to use a calculator.]
(3) Suppose this ratio is denoted by $\phi$ and take 10 cm as 1 unit then $AE$ is $\phi$ units. Show that $BE$ is $1/\phi$ units and hence $$\phi = 1 + {1\over \phi}\quad (1)$$
Explain just from equation (1), and without solving the equation, why the equation must have a solution between 1 and 2.
(4) Draw the graphs of $y=x$, $y=1/x$ and $y=1+1/x$ on the same axes and use your graph to find an approximate value for $\phi$.
(5) Solve equation (1) to find the value of $\phi$.