Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Pitchfork
Age 16 to 18
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
 |
Curt from Reigate College sent us this excellent solution. He
realised that to draw this graph you need to use the ideas
developed in the two problems
Curt sent in splendid solutions of all three problems. The
challenge was not to draw the graphs, software will do that for
you, but to explain the features of the graphs and why they have to
take the shapes they do.Well done Curt!
|
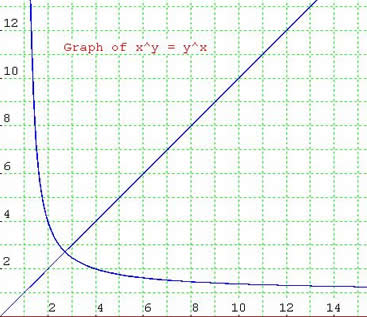
If $x^y=y^x$, before even starting I will venture that it is symmetrical on $y=x$. Why? Well because it is in fact its very own inverse. Why? By swapping $y$ and $x$, one gets the very same expression.
Secondly I say that there must be some component of the graph that resembles $y=x$. Why? Well it can clearly be seen that if $y=x=a$, the expression $a^a=a^a$ comes about. This is obviously true.
There are more subtleties at play however. Looking at the Exponential Trend graph below helps to explain the apparent hyperbola. For $x^y=y^x$, taking the $x$th and $y$th root of both sides the following equation comes about: $x^{1\over x}=y^{1\over y}$.
If one assumes that $x$ and $y$ are not equal, this equation is effectively the same as finding alternative solutions to $x^{1\over x}$ i.e. finding an $a$ not equal to $x$ for which $a^{1\over a}=x^{1\over x}$. If one were to draw a line $y=c$, this would be the same exercise as finding the $x$ intercepts of the curve $y = x^{1\over x}$ and that line.
| If such a line $y=c$ were to intercept the curve, note that there is a maximum at $x=e$. Thus, if $a^{1\over a}=b^{1\over b}$, and if $a> e$, then $b< e$ (the two intercepts either side of $e$). Also note that $a$ and $b$ are greater than one, for no matter what power you raise a number less than 1 to, the result is always less than one. As has been established, there is no $x^{1\over x}< 1$ for values of $x$ larger than one. Therefore I claim that there are no solutions to the equation $x^y=y^x$ for $x \neq y$ and $x$ and$y$ less than one. | 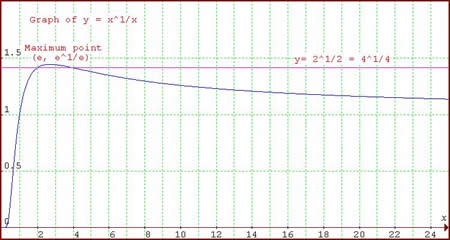 |
Furthermore, it is necessary to say that $x^y=y^x$ has AT MOST one solution for $x\neq y$. This conclusion is easily arrived at by the fact that for $x> e$, the gradient of $y=x^{1\over x}$ is always negative, thus if $y=c$ when $x=a$ and $x=b$, there is no other intercept as the curve will never equal $c$ again for $x> b$. Similarly, the gradient is always positive for $0< x< e$, thus no alternative solutions here.
Now, if there was an a such that $1< a< e$, as $a\rightarrow 1$, $y\rightarrow1$. The corresponding $b$ value would grow infinitely large as was proven above; as $x\rightarrow \infty$, $x^{1\over x} \rightarrow 1$. Thus I say that this pitchfork graph must have asymptotes at $y=1$ (and $x=1$ for we have asserted it is symmetrical).
Now, the point of symmetry. It was asserted that an $x$ value has AT MOST 2 solutions. There is a case where only one solution is possible. As was seen in Exponential Trend, the maximum of the curve occurs where $x=e$. Thus, for a $y=e^{1\over e}$, there is only 1 solution as this is the maximum. Thus I say that the only possible other solution is for $y=x$.
Anyway, I conclude that the Pitchfork graph must be symmetrical on $x=y$, it has asymptotes at $y=1$ and $x=1$, and it has a linear $x=y$ component. The components meet where $x=y=e$.
ADDITIONAL CHALLENGE
Now Curt extends this problem and sets himself a new challenge. He proves his corollary when $y$ is a multiple of $x$. Can you prove it more generally?
As a corollary, I will prove that the only integer solutions to $x^{1\over x}=y^{1\over y}$ where $x$ and $y$ are not equal are 2 and 4, i.e $2^{1\over 2} = 4^{1\over 4}$.
Let $y> x$. Let $x$ and $y$ both be integers greater than 1. Now if $x^{1\over x}=y^{1\over y}$, it follows that $x^{y\over x}=y$. Let $y/x=a > 1$ and $a$ is an integer. Let $x=1+m$ where $m$ is a positive integer. Then $$y^x = (ax)^x = x^y = x^{ax}$$ and taking the $x$th root gives: $ax = x^a$. Therefore $$ax = a(1+m) = a + am = (1 + m)^a = 1+am + \textstyle {1\over 2}a(a-1)m^2 + \cdots$$ and as $a> 1$, we can say that $a-1 \geq \textstyle{1\over 2}a(a-1)m^2$. Therefore $m \leq (2/a)^{1\over 2}$. As $a> 1$, $m\leq 1$ for we assumed $m$ is a positive integer. 1 is the largest and only possible value for $m$. Therefore $x=2$. We see that if $m=1$, $a< 3$. Now we know that $1< a< 3$ and an integer, therefore let $a=2$. Substituting this all back in we see that $2^{1\over 2}=4^{1\over 4}$.