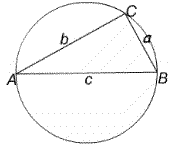
A triangle $ABC$ is inscribed in a circle with $AB$ as diameter. Find the maximum value of $AC + CB$.

Now generalise your result to the case where $AB$ is fixed but not a diameter of the circle.

Make and prove a conjecture about the cyclic quadrilateral inscribed in a circle of radius $r$ that has the maximum perimeter and the maximum area.