Efficient Cutting

'Efficient Cutting' printed from https://nrich.maths.org/

Show menu

Why do this problem?

This problem offers an opportunity for students to apply their knowledge of areas and circumferences of circles, and volumes of cylinders.

It lends itself to collaborative working, both for students who are inexperienced at working in a group and students who are used to working in this way.

Many NRICH tasks have been designed with group work in mind. Here we have gathered together a collection of short articles that outline the merits of collaborative work, together with examples of teachers' classroom practice.

Possible approach

This printable worksheet may be useful: Efficient Cutting.

This is an ideal problem for students to tackle in groups of four. Allocating these clear roles (Word, pdf) can help the group to work in a purposeful way - success on this task should be measured by how effectively the group work together as well as by the solution they reach.

Introduce the four group roles to the class. It may be appropriate, if this is the first time the class have worked in this way, to allocate particular roles to particular students. If the class work in roles over a series of lessons, it is desirable to make sure everyone experiences each role over time.

For suggestions of team-building maths tasks for use with classes unfamiliar with group work, take a look at this article and the accompanying resources.

Provide each student with a sheet of A4 paper.

"Your task is to create a cylinder with both ends closed, using only one sheet of paper. Your cylinder must not be the same as anyone else's in your group." Draw on the board, or show an image such as this one, to ensure that students are clear about the task, making it clear that there are many different cylinders that could be created. Make sure there are rulers, pairs of compasses, scissors and tape available - the resource managers in each group will be expected to equip their group appropriately.

After groups have had a chance to create some cylinders, hand out this task sheet (Word, pdf) to each group.

Make it clear that by the end of the sessions they will be expected to report back to the rest of the class with the optimum cylinder, a summary of their reasoning, and a justification that their solution can't be improved upon. Exploring the full potential of this task is likely to take more than one lesson, with time in each lesson for students to feed back ideas and share their thoughts and questions.

While groups are working, label each table with a number or letter on a post-it note, and divide the board up with the groups as headings. Listen in on what groups are saying, and use the board to jot down comments and feedback to the students about the way they are working together.

You may choose to focus on the way the students are co-operating:

Group A - Good to see you sharing different ways of tackling the problem.

Group B - Different lines of enquiry are being shared out among the group members - what an efficient way of working!

Group C - I like the way you are keeping a record of people's ideas and results.

Group D - Resource manager - is there anything your team needs?

Alternatively, your focus for feedback might be mathematical:

Group A - I like the way you are narrowing down where the circles could be drawn.

Group B - How many decimal places do you think you need for your calculations?

Group C - Good to see that someone's checking each calculation.

Make sure that while groups are working they are reminded of the need to be ready to present their findings at the end, and that all are aware of how long they have left.

We assume that each group will record their reasoning and justification on a large flipchart sheet in preparation for reporting back. There are many ways that groups can report back. Here are just a few suggestions:

Every group is given a couple of minutes to report back to the whole class. Students can seek clarification and ask questions. After each presentation, students are invited to offer positive feedback. Finally, students can suggest how the group could have improved their work on the task.
Everyone's posters are put on display at the front of the room, but only a couple of groups are selected to report back to the whole class. Feedback and suggestions can be given in the same way as above. Additionally, students from the groups which don't present can be invited to share at the end anything they did differently.
Two people from each group move to join an adjacent group. The two "hosts" explain their findings to the two "visitors". The "visitors" act as critical friends, requiring clear mathematical explanations and justifications. The "visitors" then comment on anything they did differently in their own group.

Key questions

If your focus is effective group work, this list of skills may be helpful (Word, pdf).

Ask learners to identify which skills they demonstrated, and which skills they need to develop further.

If your focus is mathematical, these prompts might be useful:

How could you arrange two circles and a suitable rectangle on the paper?

How can you be sure that you have found the optimum cylinder?

Possible extension

Cola Can provides a suitable follow-up activity.

Possible support

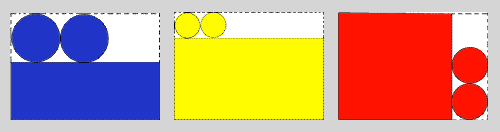
Sharing this image with students may provide inspiration for different ways of making cylinders.

If students have not met or are not confident with volume of cylinders, they could instead work on the easier problem Cuboid Challenge in the same way.