 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Where to Land



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
We had a number of correct answers to this problem. Several solutions used a spreadsheet, for example the one shown below is from an anonymous solver. We also received a solution from someone who has done some calculus and was able to solve the problem using this approach. I have included this solution at the end for those of you who are interested.
My disappointment is that some of you are still just sending in answers without explanation and I do want to see how you arrived at your answers. Although the solution below was found using a spreadsheet you might have used a calculator and carried out a standard "trial and improvement" process to obtain the same result.
Catherine, Ellean, Anna from The Mount School, York add the following comment which means they were really thinking about the numbers and the context...
How fast do you think you could run and swim in m/s?
Andisheh of Springfield School offered the following explanation (well done):
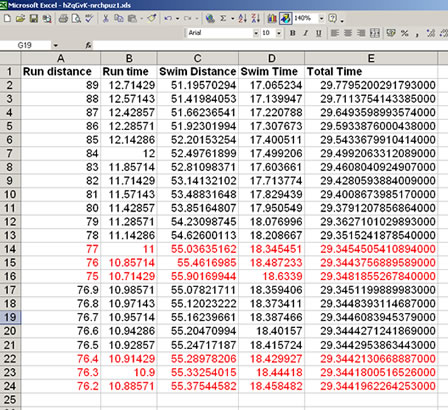
Andisheh attached a spreadsheet and I have used this and several other solutions employing a spreadhsheet to create the extract below: Solvers were able to find that the minimum time occurred with a distance between 76 and 77m and then worked with one and then two decimal places to obtain greater accuruacy.
"Swim Distance" was calculated using Pythagoras' theorem:The right-angled triangle will have sides of 50m (the distance from the beach) and $x$m, which is 100m (the distance along the beach) minus the distance run.
$$\mbox{Swim}^2 = 50^2 + x^2 $$
$$\mbox{Distance swum} = \sqrt{50^2 + x^2}$$
The times were then found in seconds by dividing the distances by the speeds and the total time just required the two times to be added.
The final solution was sent in by an anonymous solver who used calculus (a branch of mathematics normally met for the first time at advanced level in the UK). It is a neat solution but this high level mathematics was certainly not required!
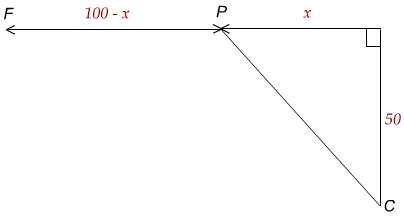
Let $T$ be the total time.
Let $t_1$ be the time spent swimming.
Let $t_2$ be the time spent running.
By Pythagoras' theorem
\begin{eqnarray} PC^2 &=& 50^2 + x^2 \\ PC&=& \sqrt{50^2 + x^2} \end{eqnarray}
So for the total time:
$$ T = \frac{\sqrt{x^2 + 50^2}}{3} + \frac{100-x}{7}$$
$$\frac{dT}{dx} = \frac{x(x^2 + 50^2)^\frac{-1}{2}}{3}- \frac{1}{7}$$
$$\frac{dT}{dx} = 0 \mbox{ when } \frac{1}{7} = \frac{x(x^2 + 50^2)^\frac{-1}{2}}{3}$$ Important question to think about:
How would you check that this is a minimum value?
Solving the equation above for $x$
\begin{eqnarray} 3(x^2+50^2)^\frac{1}{2} &=& 7x\\ 9(x^2+50^2)&=& 49x^2\\ x&=& 23.7 \mbox{ (1dp)} \end{eqnarray}
Chris will need to land at the point on the beach 76.3m from the family.
You may also like
Some(?) of the Parts
A circle touches the lines OA, OB and AB where OA and OB are perpendicular. Show that the diameter of the circle is equal to the perimeter of the triangle
Ladder and Cube
A 1 metre cube has one face on the ground and one face against a wall. A 4 metre ladder leans against the wall and just touches the cube. How high is the top of the ladder above the ground?
At a Glance
The area of a regular pentagon looks about twice as a big as the pentangle star drawn within it. Is it?