You may also like

problem icon

Transformations on a Pegboard

How would you move the bands on the pegboard to alter these shapes?

problem icon

Fred the Class Robot

Billy's class had a robot called Fred who could draw with chalk held underneath him. What shapes did the pupils make Fred draw?

problem icon

Triangles All Around

Can you find all the different triangles on these peg boards, and find their angles?

Cartesian Isometric

Stage: 2 Challenge Level: Challenge Level:3 Challenge Level:3 Challenge Level:3

The graph below is a coordinate system based on $60$ $^\circ$ angles. It was drawn on isometric paper.

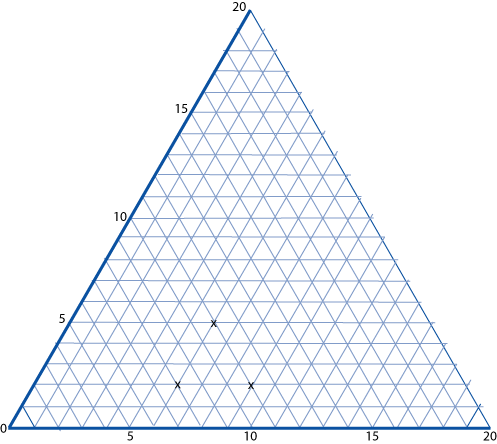
The marked points are $(6, 2)$, $(6, 5)$ and $(9, 2)$. When joined they form an equilateral triangle.

The following five sets of points are also triangles.

A. $(1, 13), (6, 8)$ and $(6, 13)$.
B. $(1, 1), (3, 3)$ and $(7, 1)$.
C. $(12, 1), (17, 1)$ and $(8, 9)$.
D. $(1, 10), (5, 2)$ and $(6, 6)$.
E. $(7, 5), (15, 4)$ and $(7, 11)$.

What kinds of triangles are they?
Can you work out any of the angles at the vertices?



The NRICH Project aims to enrich the mathematical experiences of all learners. To support this aim, members of the NRICH team work in a wide range of capacities, including providing professional development for teachers wishing to embed rich mathematical tasks into everyday classroom practice. More information on many of our other activities can be found here.
Copyright © 1997 - 2012. University of Cambridge. All rights reserved.
NRICH is part of the family of activities in the Millennium Mathematics Project.