Sending a Parcel printable sheet

The Post Office used to have a strange way of limiting the size of parcels. The maximum allowed was "6 feet combined length and girth". That meant you added together the distance round the middle of the parcel (that's the girth) and the length.

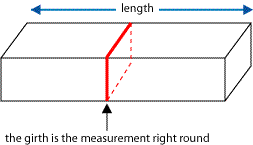
You could have sent a fishing rod very nearly 6 feet long and just a few inches round the girth!

Bringing the problem up-to-date, let's set the maximum combined length and girth to be 2 metres (which is a bit more than 6 feet).

What is the greatest volume you can now get for a cuboid parcel with whole centimetre dimensions?