Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
The Money Maze
Age 7 to 11
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
The Money Maze
Go through the maze, collecting and losing your money as you go. You may not go through any cell more than once, and can only go into a cell through a gap, for example, you may not go from $5$ to $6$, or from $7$ to $3$.
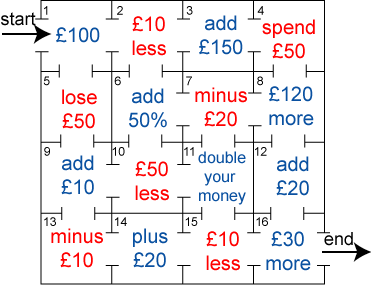
Which route gives you the highest return? How much is it?
Which route gives you the lowest return? How much is it?
Why do this problem?
This problem gives learners the opportunity to practice addition, subtraction, multiplication and division of money, while it includes calculating with percentage. It is also a good context for developing a recording system and a systematic approach.
Possible approach
Pupils will need to develop their own recording system to show which routes they have tried. Encourage them to discuss how they know they have tried the different options so that they begin to see the need for a systematic approach.
This sheet has two copies of the maze on it.
Key questions
Have you thought of a way of recording the routes you have found?
How do you know that you have tried all the different ways through the maze?
How many ways are there to go from the first square?
Which one will you try first?
Are you sure there is a gap to go through between those two squares?