Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Circles Ad Infinitum
Age 16 to 18
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Thank you Tom
from Wolgarston High School, Hidayah who does not name a school,
Hamish and Jared from Ulverston Victoria High School, Eduardo from The
British School, Manila, Justin from Skyview High School, Billings, MT
USA and Fabian from Sabino High School in Tucson, Arizona,
U.S.A. for sending your very good solutions to this problem.You all
tackled the problem in a similar way. 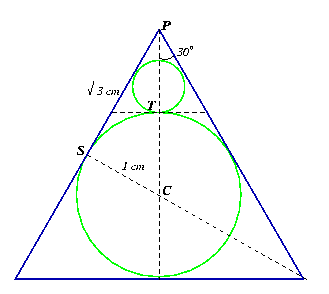
Let $C$ be the centre of the central circle. Then $PS$ is a
tangent to this circle. Then triangle $CSP$ is a 30-60-90 triangle
and, given that $CS = 1 $ cm, it follows that $PS = \sqrt{3}$ cm
and $PC = 2$ cm. Hence the height of the largest equilateral
triangle is $3$ cm. ($PC$ + radius of $ 1$ cm.), the height of the
next size equilateral triangle is $1$ cm. ($PC$ - radius of $1$
cm.) and the radius of the next size circle is $1/3$ cm.
Each circle is scaled down by a linear scale factor of $1/3$
and by an area scale factor of $1/9$.
There is one central circle and at each stage after that 3 new
circles are added.
The 'total circumference' is the sum of the circumferences of
all the circles, given by:
Total circumference = $ 2\pi + 3 ({ 2\pi\over 3} + {2\pi\over
9} + {2\pi \over 27}+ \ldots ) $
where the dots denote that the sum goes on for ever. Summing
this infinite geometric series gives: $$ \mbox{Total circumference}
= 2\pi + 2\pi (1 + {1\over 3} + {1\over 9} + {1\over 27} + \ldots )
= 2\pi + \frac{2\pi}{1 - 1/3} = 5\pi $$ The 'total area' is the sum
of the areas of all the circles, given by:
Total area = $ \pi + 3 ({\pi\over 9} + {\pi\over 9^2} + {\pi\over 9^3} + \ldots )$
where the dots denote that the sum goes on for ever. Summing
this infinite geometric series gives: $$ \mbox{Total area} = \pi +
{\pi\over 3} (1 + {1\over 9} + {1\over 9^2} + \ldots ) = \pi +
\frac{\pi}{3(1 - 1/9)} = \frac{11\pi}{8} $$ Clearly, the total of
the circumferences grows faster than the total of the areas because
the scale factor 1/3 is bigger than the scale factor 1/9.