Circles Ad Infinitum
A circle is inscribed in an equilateral triangle. Smaller circles touch it and the sides of the triangle, the process continuing indefinitely. What is the sum of the areas of all the circles?
Problem
A circle of radius 1 cm is inscribed in an equilateral triangle. A smaller circle is inscribed at each vertex touching the first circle and tangent to the two 'containing' sides of the triangle. This process is continued ad infinitum....

What is the sum of the circumferences of all the circles?
What is the sum of their areas?
Adding all the circumferences or adding all the areas, which sum grows faster?
Getting Started
Can you spot your old friend the 30-60-90 triangle? Then you are into scaling down and geometric series.
Student Solutions
Thank you Tom from Wolgarston High School, Hidayah who does not name a school, Hamish and Jared from Ulverston Victoria High School, Eduardo from The British School, Manila, Justin from Skyview High School, Billings, MT USA and Fabian from Sabino High School in Tucson, Arizona, U.S.A. for sending your very good solutions to this problem.You all tackled the problem in a similar way.
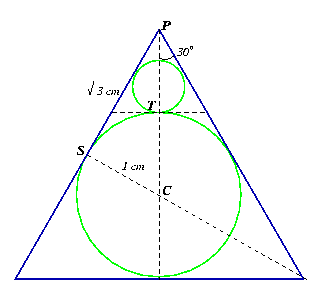
Total area = $ \pi + 3 ({\pi\over 9} + {\pi\over 9^2} + {\pi\over 9^3} + \ldots )$
Teachers' Resources
Why do this problem?
Scaling is a key idea in mathematics and this problem provides good practice in working with this concept and in summing geometric series. Enjoy the idea of being able to get a hold on an infinite process in a concrete way.
Possible approach
First ask the learners to work out the radius, circumference and area of the first three circles. (It is often a good strategy in problem solving to concentrate on $n=1$ first).
Then ask them to work out the radii of the next few circles; this will concentrate the thinking on scaling.
Then ask them to to work out circumferences and add them up; this will concentrate the thinking on summing series.
Key questions
Can you work out the radii of the circles?
What are the scale factors?
If you sum the circumferences what sort of series do you get?
If you sum the areas what sort of series do you get?
Can you sum these series?
Possible extension
Try the problem Von Koch Curve.
Possible support
Try the problem Smaller and Smaller.
